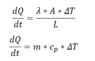Fritiofmikael
- 4
- 0
Hi,
I have been trying to set up a funtcion of the temperature over time and I am doubting my results.
In the system i have:
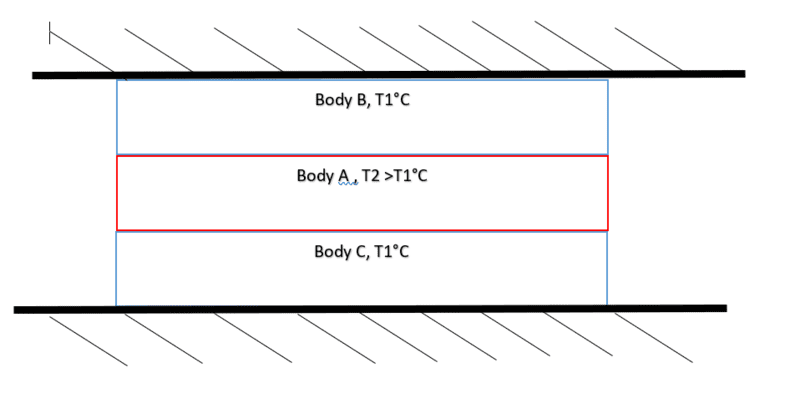
Fig 1.
The system is at rest. For simplicty I've considerd the ambient temperature to be same as T1.
By knowing:
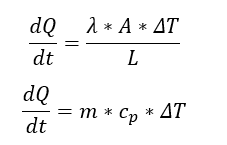
Fig 2.
yeilds:
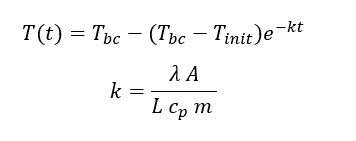
Fig 3.
In my case B&C is at a constant Temperature of 15°C and Body A 115°C.
The specific heat cond and heat transfer coeff for A is:
0,19 W/m
1700 J/kg
For A:
Length = 2.41m
Width = 2.071m
Depth = 0.01m
Density = 950 kg/m3For Fig3. i end up with L=0.01m A=0.0207m2 and m = 47.4 kg.
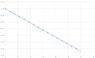
By using the function above and plotting over 60 sec i get.
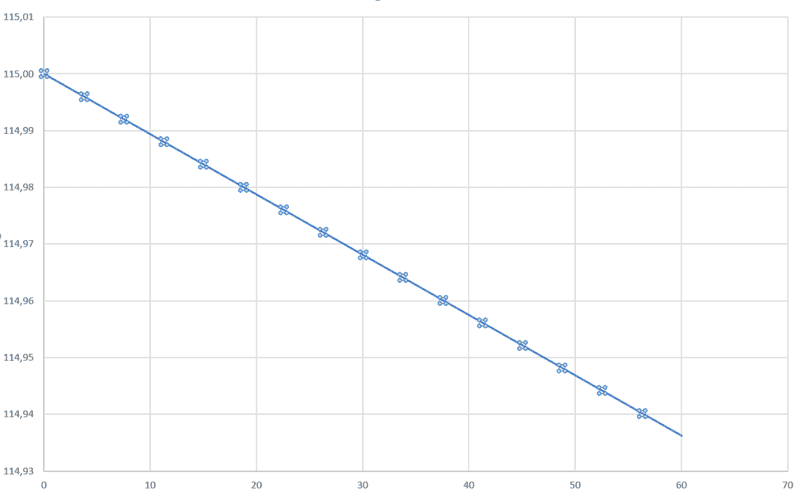
Fig 4
I'm not satisfied with my end result and wondering if anyone can see if there are any obvious errors?
Best Regards
Mikael
I have been trying to set up a funtcion of the temperature over time and I am doubting my results.
In the system i have:
Fig 1.
The system is at rest. For simplicty I've considerd the ambient temperature to be same as T1.
By knowing:
Fig 2.
yeilds:
Fig 3.
In my case B&C is at a constant Temperature of 15°C and Body A 115°C.
The specific heat cond and heat transfer coeff for A is:
0,19 W/m
1700 J/kg
For A:
Length = 2.41m
Width = 2.071m
Depth = 0.01m
Density = 950 kg/m3For Fig3. i end up with L=0.01m A=0.0207m2 and m = 47.4 kg.
By using the function above and plotting over 60 sec i get.
Fig 4
I'm not satisfied with my end result and wondering if anyone can see if there are any obvious errors?
Best Regards
Mikael
Attachments
Last edited: