Heat transfer problem for a long rectangular bar

[Nusselt]

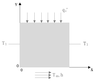
Summary:: Determine the temperature distribution in a bar (very long– 2D) with rectangular cross section, in steady state, with imposed flux at one face, convection at the opposing face (Tinf, h), and imposed temperature (T1) at the two remaining walls.

I am trying to find the analytical solution to the following problem :

Determine the temperature distribution in a bar (very long– 2D) with rectangular cross section, in steady state, with imposed flux at one face, convection at the opposing face (Tinf, h), and imposed temperature (T1) at the two remaining walls.

I have the differential equation and four boundary conditions , however I can't find the temperature distribution even using the supeposition method ( trying to find the solution with one of the walls adiabatic and the other transferring energy by convection and then finding the solution for one of the walls adiabatic and the other with imposed flux).

Has anyone came across a problem like this?

 

[Chestermiller]

Your figure matches the problem statement, but there are no adiabatic walls mentioned in the problem statement.

 

[Nusselt]

Your figure matches the problem statement, but there are no adiabatic walls mentioned in the problem statement.

I was describing how i was using the superposition method

 

[Chestermiller]

I like your approach. How do you handle the other two boundaries in each of the two cases?

 

[Chestermiller]

You are on the right track. Instead of using 2 superpositions, use three. The first case is where T is equal to T1 everywhere and the flux ends are both insulated. The other two cases are the ones you already described, but with zero temperatures where T1 had been. These two other cases can be solved by separation of variables, with sine series in the x direction and hyperbolic sines and cosines in the y direction.