Heliocentric polar orbit crossing the Earth's orbit twice

[xpell]

Sorry, the title's length didn't allow me to explain this better and I need it for a story that I'm writing, if you're so kind to help me. I've been trying it hard to solve it myself but I've been unable to.

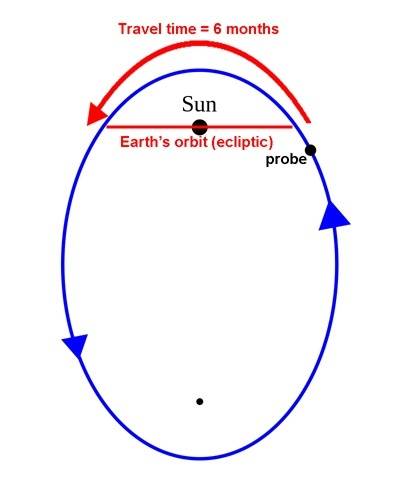
The problem looks simple but it isn't (for me): Please assume we have a space probe of negligible mass in a highly eccentric, heliocentric polar orbit (so it doesn't experience heavy perturbation caused by other solar system bodies; let's say it "goes up and down" the Sun.) I need this probe to "meet" (experience a close encounter with) the Earth twice every time it travels along the perihelion (i.e. 6 months of travel between each extreme of the Sun-focus latum rectum), like in this drawing:

Could anyone please help me to solve the following:?

• Dimensions of the ellipse (major and minor axis and/or eccentricity);
• Total orbital period;
• Maximum velocity at the perihelion; and, most important:
• Velocity (relative to the Earth) while "crossing" the Earth's orbit "upwards" and, 6 months later, "downwards."

Thank you in advance for any help! (And please move if this is not the appropriate forum...)

 

[mfb]

In an eccentric orbit, the probe would have both a shorter path and a higher speed than Earth. To make that work, the probe needs a nearly circular orbit similar to the one of Earth.

The close encounters with Earth will make the orbit unstable.

 

[xpell]

Thank you, Mfb!

The close encounters with Earth will make the orbit unstable.

Let's assume that the probe has some maneouvering/stationkeeping capability to compensate this, please.

In an eccentric orbit, the probe would have both a shorter path and a higher speed than Earth. To make that work, the probe needs a nearly circular orbit similar to the one of Earth.

Heck, I didn't think so, but you're most probably right... is there any formula or something that I could use to calculate that, please?

And no highly eccentric orbit that would cover the "perihelion leg" in such a time because of a very high velocity (even if the perihelion is quite far away!)?

 

[mfb]

Note: the Earth has a slightly eccentric orbit (0.017), I'll ignore this here, it does not change the conclusions.

And no highly eccentric orbit that would cover the "perihelion leg" in such a time because of a very high velocity (even if the perihelion is quite far away!)?

The perihelion has a maximal distance of 1 AU, otherwise your orbit doesn't cross the one of Earth. A circular orbit with a radius of 1 AU matches your required time, everything else does not.

There are formulas to calculate things like the time spent between two points of the orbit, and various websites show to calculate that. It's not necessary in this case.

Unrelated: to make it worse, to match the orbital period, the semi-major axis has to be the same. An eccentric orbit out of the plane of the planets with the same semi-major axis as Earth cannot cross its orbit twice.

Let's assume that the probe has some maneouvering/stationkeeping capability to compensate this, please.

Hmm...

 

[xpell]

Note: the Earth has a slightly eccentric orbit (0.017), I'll ignore this here, it does not change the conclusions.
The perihelion has a maximal distance of 1 AU, otherwise your orbit doesn't cross the one of Earth. A circular orbit with a radius of 1 AU matches your required time, everything else does not.

There are formulas to calculate things like the time spent between two points of the orbit, and various websites show to calculate that. It's not necessary in this case.

Of course you're right, Mfb. Silly me didn't notice on the spot that my only possible orbit is another "Earth's orbit" more or less inclined relative to the ecliptic, does it?

Unrelated: to make it worse, to match the orbital period, the semi-major axis has to be the same. An eccentric orbit out of the plane of the planets with the same semi-major axis as Earth cannot cross its orbit twice.

Hmm...

Just out of curiosity, would you be so kind to elaborate this a bit more please? I'm interested!

 

[mfb]

my only possible orbit is another "Earth's orbit" more or less inclined relative to the ecliptic, does it?

Right.

Just out of curiosity, would you be so kind to elaborate this a bit more please? I'm interested!

Draw an ellipse and a circle with the same semi-major axis and focal point on a plane. They will intersect each other twice, but the intersection points are not on opposite sides of the central body. There is no way to rotate the ellipse out of the plane while keeping the two intersection points. You can rotate around the (sun - one intersection) axis, but then the second intersection goes away.

 

[xpell]

Draw an ellipse and a circle with the same semi-major axis and focal point on a plane. They will intersect each other twice, but the intersection points are not on opposite sides of the central body. There is no way to rotate the ellipse out of the plane while keeping the two intersection points. You can rotate around the (sun - one intersection) axis, but then the second intersection goes away.

Done and understood. Thank you very much, Mfb. :)

 

[BobG]

The problem looks simple but it isn't (for me): Please assume we have a space probe of negligible mass in a highly eccentric, heliocentric polar orbit (so it doesn't experience heavy perturbation caused by other solar system bodies; let's say it "goes up and down" the Sun.) I need this probe to "meet" (experience a close encounter with) the Earth twice every time it travels along the perihelion (i.e. 6 months of travel between each extreme of the Sun-focus latum rectum), like in this drawing:

Can't happen. If it's orbital period is half the Earth's orbital period, then the orbit has to be smaller and perigee will be closer to the Sun than the Earth.

You could set up an orbit that has half the Earth's orbital period and is close to the Earth at apogee. But every other orbit, the Earth won't be there - the Earth will be on the other side of the Sun.

As mentioned, the only way to get close to the Earth twice a year is to have a circular orbit the same size as the Earth.

 

[xpell]

Can't happen. If it's orbital period is half the Earth's orbital period, then the orbit has to be smaller and perigee will be closer to the Sun than the Earth.

You could set up an orbit that has half the Earth's orbital period and is close to the Earth at apogee. But every other orbit, the Earth won't be there - the Earth will be on the other side of the Sun.

As mentioned, the only way to get close to the Earth twice a year is to have a circular orbit the same size as the Earth.

Thank you too very much, BobG. :)