B The Sun's Influence on the Moon's Orbit: Is it Negligible?

[LesRhorer]

TL;DR Summary

In another thread it was stated the Sun's effect on the moon is negligible. Nope.

Do the math, folks. The Moon travels a path apparently around the Earth with an orbital amplitude of roughly 800,000 Km. In reality, the Moon travels around the Sun, and the Earth has a significant, but smaller influence on the Moon. The Sun's gravitational influence on the Moon is nearly twice the Earth's influence. (Roughly 1.9185, to be more precise) Since to first approximation, however, the Earth and Moon are traveling in the same gravitational field, so their motion WRT each other is nominally uniform. The Sun's influence on the Moon's orbit is not completely insignificant, however, and certainly not unmeasurable. The mean gravitational field strength of the Sun at the Earth-Moon orbit is given by Newton's Universal Law of Gravitation:

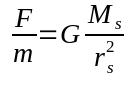
Plugging in the numbers, we find the average solar field strength to be around 0.0059 N/Kg. The tidal potential is certainly not zero, however, so the Moon's apparent orbit around the Earth is not the perfect ellipse it would be if the Sun weren't there. The tidal variation is roughly 6.294 x10⁻⁵ N/Kg or about 1%. That is certainly not huge, by any means, but I wouldn't call it insignificant, either. The Sun tides on Earth are not huge, either, butt hey are certainly noticeable and measurable, and that is over a tidal span of a mere 8000 Km, compared to 800,000 Km for the Moon, and for a body (the oceans) where the terrestrial gravitational field strength is some 1 million times greater.. In any case, the result is a bulge in what would normally be a nice, near circular ellipse. At the Moon's orbit, the terrestrial gravitational field strength is 3.076 x 10⁻³N/Kg. At the sub-solar point in the Moon's orbit about the Earth, that number is reduced to 3.044 x 10⁻³N/Kg by the Sun's gravity, resulting in a small, but quite measurable, increase in the distance to the Moon not related to the normal eccentricity of its orbit, and a slight, but again measurable, slow down of the Moon's velocity WRT Earth. Certainly this is not evident to the naked eye, or even to a consumer grade telescope, but since we can take cm resolution measurements of the distance to the Moon, its as, as I say, quite measurable. The Sun distorts the orbit of the Moon.

If someone attached a giant rocket to the Moon and created a constant force along the orbital path WRT the Earth, the Moon's orbit would begin to grow and its orbital speed would begin to drop. The bulge would also grow larger and larger. At some point, the Moon's orbit would eventually intersect the L1 Lagrange point, and the Sun would then rip the Moon totally away from the Earth. Note to the Moon, other than no longer having the Earth fill up a significant chunk of sky, not much would be happening. It would be somewhat closer to the Sun, and its orbit around the Sun would have a shorter period, and that orbit would be just a tiny bit flatter than before, but its principal planetary governor would still be the Sun. It will have gotten rid of the little pipsqueak that jostled it around all the time.

(Someone might care to check my math, here. I checked it twice, and found one mistake before I posted, but of course there could be some error I did not catch.)

 

[PeroK]

https://van.physics.illinois.edu/ask/listing/18501

 

[PeroK]

PS it's negligible in the sense that the Sun is not a primary factor in the Moon's orbit. This is despite the Sun's gravity on the Moon being stronger than the Earth's gravity. That was the context of the quotation. To counter the argument that the Sun's gravitational field strength is the critical factor in orbits around a planet.

It's a subsidiary factor of course.

 

[Dale]

The actual quote is:

Just to add that, AFAIK, the Sun has an almost negligible effect on the orbit of the Moon about the Earth.

Meaning that the "orbit of the Moon about the Earth" would be about the same with or without the Sun. The claim is that the orbital parameters of the Moon with respect to the Earth are negligibly affected by the presence of the sun. I don't know if it is correct, but is a different claim than what you posted. The forum's built-in quote feature is intended to allow accurate quotations and to allow participants to go back and see the quote in context.

Please do not re-open closed threads and please do not misquote people.

 

[Drakkith]

I know this thread is closed, but I wanted to point out that it might be more helpful for everyone if you make sure you understand what someone means before you make a full rebuttal of their point. This entire thread happened because you didn't ask what PeroK meant by 'negligible effect'. Yes, the Sun has an effect on the Moon's orbit. Yes, that effect is easily measurable and calculable. But to PeroK it is negligible in the context of his original point.

If someone is studying the gravitational acceleration of various bodies upon the Moon's orbit around the Sun, then yes, the Sun would be the dominant factor and absolutely not negligible. But for its orbit around the Earth the Moon is far more influenced by the Earth than by the Sun.

Do the math, folks.

I assure you, we are not stupid. We have done the math plenty of times before. If you would focus on understanding and learning instead of winning an argument you will likely do far better here at PF.