Help a chair leaning 60 degrees against a wall

[Science4ver]

Homework Statement

Hi guys,

I have a problem here.


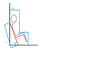
A man is sitting on a chair leaning at 60 degrees against a friction-less wall. The height of the chair is 1.20 meters and the distance between the man's center of mass and the wall is 0.5 meters. The distance between the guy's knees and the floor while the chair is leaning is 0.9 meters.

The weight of man + chair is 80 kg. Note the guy is assumed to be sitting still and will be moving while leaning against the wall.

1) Calculate the force between man+chair and the wall and calculate the force between man+chair and the floor.

Homework Equations

Newton 2. law

The Attempt at a Solution

In order to calculate these force I use the equilibium equations.

Thusly \sum F_y = m_{c+m} \cdot g \cdot sin(60) \cdot 1.2 - F_{wall}=0

and \sum F_x = m_{c+m} \cdot g \cdot cos(60) \cdot 0.5 - F_{floor}=0


and I on the right track here guys?

 

[verty]

Do you understand the relevance of the wall having no friction? Why is this important?

 

[Science4ver]

Do you understand the relevance of the wall having no friction? Why is this important?

I think so. I think it that means that the chair will stay in place because the wall is frictionless?

 

[PhanthomJay]

It appears your sketch is out of scale. The cg of the mass-chair is closer to the wall than the support leg of the chair. Your sketch shows otherwise. Try summing torques about the support leg, after first determining the value of the vertical force at the wall on the chair based on a frictionless wall which should tell you something about that force.

 

[Science4ver]

It appears your sketch is out of scale. The cg of the mass-chair is closer to the wall than the support leg of the chair. Your sketch shows otherwise. Try summing torques about the support leg, after first determining the value of the vertical force at the wall on the chair based on a frictionless wall which should tell you something about that force.

You mean like if

\sum \tau = 0: \tau_{ccw} = \tau_{cw}

and thusly formula for calculating the force from the wall is

F_{wall} \cdot L_{latter} \cdot sin(\theta) = F_{G} \cdot d_{cg} \cdot sin(\alpha)

where alpha is the top angle in the triangle in drawing.

 

[PhanthomJay]

What is direction of F_wall? Note also the moment of a force about a point is fjor ce times perpendicular
Distance from line if its action to point.

 

[Science4ver]

Its to the right from wall like the force of friction.

 

[PhanthomJay]

Yes it acts to the right perpendicular to the wall (it is a "Normal" force). Friction forces act parallel to the surface (vertical in this case). Since the wall is frictionless, is there a vertical force at this point?

 

[Science4ver]

F_G?

 

[PhanthomJay]

There is a vertical force equal to the weight of the man and chair that acts upward on the chair leg from the floor. There can be no vertical force at the wall and chair top interface because the frictionless wall will not allow it. So sum moments about the chairleg/floor point to solve for F_wall. Your first term was correct. But the moment of the weight was not.

 

[Science4ver]

Which first term are you referring to?

 

[PhanthomJay]

F_wall(L)sin theta is the moment of the wall force about the point where the leg of the chair meets the floor. That part is correct. Clockwise. Now what is the moment of the weight force ccw about that point? Don't forget to correct your sketch. And note moment is force times perpendicular distance.

 

[verty]

I don't think this is helping Science4ver. No serious attempt has been made and the answers given were not nearly correct. Better to leave it.

 

[Science4ver]

I am not sure here is it then just

F_G * sin (theta) and do I need to multiply this with the distance betweem the chair's leg and the wall?