Help finding the angle between the force vector and line AO

[Frankenstein19]

Homework Statement

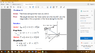
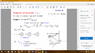
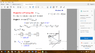
Find: The angle between the force vector and the line AO, and the magnitude of the projection of the force along the line AO

Homework Equations

cos(theta)=(A*B)/(|A|*|B|)

The Attempt at a Solution

I thought that since I'm given the force F in cartesian form, that I would need to calculate the component of the force F on the line AO and then use the cos(theta)=(A*B)/(|A|*|B|) but that's not at all what my professor did or what I see other people doing.

I first calculated r_ao and got -1i+2j-2k and its magnitude to be 3m

Then I got the magnitude component of F along AO by finding the unit vector of rao and multiplying that using the dot product with F

Then now that I have the magnitude of FAO and the positio vector rao I thought I could then calculate FAO in cartesian vector form and THEN I thought I had everything I needed to get the angle by using
cos(theta)=(A*B)/(|A|*|B|) but I'm not getting the right answer

Can someone please tell me what I'm doing wrong

*Also I'm sorry about uploading so many attachments, I always have problems adding pictures and I don't know hot to remove the excess attachments*

 

[TSny]

Your method should get the correct answer for theta. If it didn't, show your work so we can see the steps in detail.

Note that when using cos(theta)=(A*B)/(|A|*|B|) to find theta, you will get the same answer for theta if you replace the vector B by any other vector that has the same direction as B.

In your problem, the vector A is the force vector F. You teacher used the vector AO for B. You want to use the projection of F onto AO for B (where this projection is a vector in the same direction as AO). So, you should get the same answer for theta. You would also get the same answer for theta if you used the unit vector along AO for B.

 

[Frankenstein19]

Your method should get the correct answer for theta. If it didn't, show your work so we can see the steps in detail.

Note that when using cos(theta)=(A*B)/(|A|*|B|) to find theta, you will get the same answer for theta if you replace the vector B by any other vector that has the same direction as B.

In your problem, the vector A is the force vector F. You teacher used the vector AO for B. You want to use the projection of F onto AO for B (where this projection is a vector in the same direction as AO). So, you should get the same answer for theta. You would also get the same answer for theta if you used the unit vector along AO for B.

Thank you so much for answering. I'm going to show my work:irst I found the position vector rao, since the coordinates of A are (1, -2, 2) and O (0,0,0) the position vector is (0-1)i + (0+2)j + (0-2) which gives me -1i +2j -2k for rao.

Then I calculated the magnitudeand got 3m.

The unit vector for rao: -1/3i +2/3j -2/3k which is -0.33i + 0.67j - 0.67k

to get the component of F along AO I used the dot product with the cartesian vector F and with the unit vector of rao and got (-6i +9j +3k) dot -0.33i + 0.67j - 0.67k which gives me 1.98 + 6.03 -2.01= 6, this is I know is the magnitude of FAO, so to get FAO in cartesian vector form I multiplied -1i +2j -2k by 6 giving me -6i + 12j -12k as FAO in cartesian vector form.

the dot product of FAO and F gives me (-6i + 12j -12k) dot (-6i +9j +3k) = 108

cos(theta)=(A*B)/(|A|*|B|) = 108/(3*11.22) = 3.21

the arccos of that is invalid

 

[TSny]

I found the position vector rao, since the coordinates of A are (1, -2, 2) and O (0,0,0) the position vector is (0-1)i + (0+2)j + (0-2) which gives me -1i +2j -2k for rao.

OK

Then I calculated the magnitudeand got 3m.

The unit vector for rao: -1/3i +2/3j -2/3k which is -0.33i + 0.67j - 0.67k

OK

to get the component of F along AO I used the dot product with the cartesian vector F and with the unit vector of rao and got (-6i +9j +3k) dot -0.33i + 0.67j - 0.67k which gives me 1.98 + 6.03 -2.01= 6, this is I know is the magnitude of FAO,

OK

so to get FAO in cartesian vector form I multiplied -1i +2j -2k by 6 giving me -6i + 12j -12k as FAO in cartesian vector form.

Shouldn't you use the unit vector along AO rather than AO itself in order to get the vector FAO?

the dot product of FAO and F gives me (-6i + 12j -12k) dot (-6i +9j +3k) = 108

cos(theta)=(A*B)/(|A|*|B|) = 108/(3*11.22) = 3.21

If A = -6i + 12j -12k and B = -6i +9j +3k, then A dot B is 108, as you found. But note that the magnitude of A is not 3.

For any arbitrary vectors A and B you should always find that (A*B)/(|A|*|B|) is less than or equal to 1.

 

[Frankenstein19]

OK

OK

OKShouldn't you use the unit vector along AO rather than AO itself in order to get the vector FAO?If A = -6i + 12j -12k and B = -6i +9j +3k, then A dot B is 108, as you found. But note that the magnitude of A is not 3.

For any arbitrary vectors A and B you should always find that (A*B)/(|A|*|B|) is less than or equal to 1.

Ohhh yes I don;t know why I was using the position vector instead of the unit vector to find the force vector. Thank you so much for helping me <3