Help identifying a zero-force member

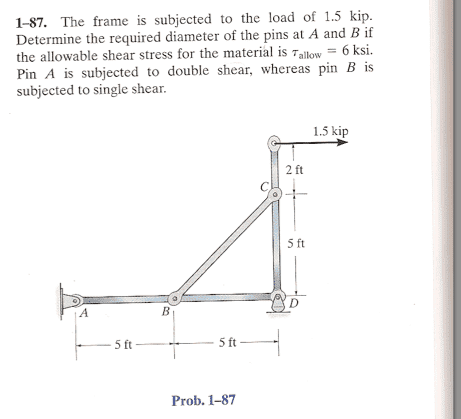
[Saladsamurai]

So I know the that the general rule for identifying a zero force member is that if two members form a joint and no external loading or reaction forces are applied to the joint then the members must be zero force members.

And if three members form a joint for which two are collinear, then the 3rd is zero force provided there is no external/reaction forces at the joint.

BUT in the following case how would one know that the joint at member CK is zero force?

There are four members at the joint, so neither general rule can be applied.

I mean, what would "tip me off"? And how would I prove it is zero force?

 

[Saladsamurai]

Wow. This must be a tough one. Anyway. Looking at Joint K we would have $$\sum F_y=F_{kb}_y+f_{ck}=0$$ so this doesn't tell me anything. Looking at joint C we would have $$F_{ck}+4+F_{cj}_y=0$$. . . great, now what?. . . hmmm let me think.

Any ideas?

 

[Saladsamurai]

god damnit