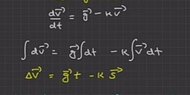Help me to understand how integrating this function works

[Kalarudra]

TL;DR

Why picture 1 can integrate the acceleration without moving (g-kV) to the dv segment? I tried to prove it if it's true by doing something similar in figure 2 but the integral result shows a difference between the left and right sides so am I wrong? then what conditions must be met in the integral operation so that image one can be said to be correct

Picture 1

Picture 2

 

[BvU]

Please check the PF guidelines -- your post is hard to understand

... by doing something similar in figure 2 but the integral result shows a difference between the left and right sides so am I wrong?

Please explain what you are doing here:

In the first step one would expect $$\int \sqrt{4v+1} \, dt$$ ($dt$, not $t$) which with $v = t^2 + t$ (dependent on $t$, so not a constant that can be taken out of the integral) would become $$\int \sqrt { 4 t^2+ 4t +1} \, dt =\frac {t(t+1)\sqrt{(2t+1)^2} }{2t+1}$$ and now $\int_0^1=2$ as expected

$\$

 

[Ibix]

Is the first approach not just integrating both sides with respect to $t$ and using that $\int_{t=t_0}^{t_1}\frac{dv}{dt}dt=\int_{v=v(t_0)}^{v(t_1)}dv$ to simplify the left hand side? I'm sure you can do it by other methods if you want.

 

[Kalarudra]

:selamat datang:

Silakan periksa pedoman PF -- postingan Anda sulit dipahami


Tolong jelaskan apa yang Anda lakukan di sini:

View attachment 357049​

Pada langkah pertama, kita akan mengharapkan $$\int \sqrt{4v+1} \, dt$$ ($dt$, bukan $t$) yang dengan $v = t^2 + t$ (bergantung pada $t$, jadi bukan konstanta yang dapat dikeluarkan dari integral) akan menjadi $$\int \sqrt { 4 t^2+ 4t +1} \, dt =\frac {t(t+1)\sqrt{(2t+1)^2} }{2t+1}$$ dan sekarang $\int_0^1=2$ seperti yang diharapkan

$\$

Sorry i tried to integrate the acceleration equation with respect to v that i got, but why i cant get same answer when i used v=2 without Spell out V into v equation with respect to t

 

[Kalarudra]

Sorry i tried to integrate the acceleration equation with respect to v that i got, but why i cant get same answer when i used v=2 without Spell out V into v equation with respect to t

In picture 1 there is acceleration equation with respect to v. When it will integrate dv alone and dt moved to other side joint with g-kv. and after integrating the equation the result is v=gt-kS that S is the trajectory. Is it correct?

 

[kuruman]

In addition to what has already been said, note that
1. You can drop the vector signs and write $$\frac{dv}{dt}=g-\kappa v.$$ 2. You have two variables, $v$ and $t$ which you must separate before integrating. To separate means to have variables of only one kind on each side and write $$\frac{dv}{(g-\kappa v)}=dt.$$ You can now integrate because you have separated variables. Don't forget that integration is basically a summation so when you add things together they must be of the same kind and not a mixture of two.

 

[Kalarudra]

In addition to what has already been said, note that
1. You can drop the vector signs and write $$\frac{dv}{dt}=g-\kappa v.$$ 2. You have two variables, $v$ and $t$ which you must separate before integrating. To separate means to have variables of only one kind on each side and write $$\frac{dv}{(g-\kappa v)}=dt.$$ You can now integrate because you have separated variables. Don't forget that integration is basically a summation so when you add things together they must be of the same kind and not a mixture of two.

Please see picture 1 can you explain it? is it true?

 

[kuruman]

Please see picture 1 can you explain it? is it true?

It is true but it is not very useful. I would assume that the question is to find the velocity as a function of time in which you have $v$ on the left hand side and constants and $t$ on the right hand side. This expression has $s$ on the right hand side which not constant but depends on time $t$ in some way that needs to be determined.

 

[Kalarudra]

It is true but it is not very useful. I would assume that the question is to find the velocity as a function of time in which you have $v$ on the left hand side and constants and $t$ on the right hand side. This expression has $s$ on the right hand side which not constant but depends on time $t$ in some way that needs to be determined.

But in picture 2 i try to integrate function of acceleration why i didnt got same answer is there any false integrating that i do? I know i had typo when i integrating the function i wrote t that should be dt. But the answer always same

 

[kuruman]

But in picture 2 i try to integrate function of acceleration why i didnt got same answer is there any false integrating that i do?

The same answer as what?

Picture 1 and picture 2 are completely different. In picture 1 you have $a=\dfrac{dv}{dt}=g-\kappa v$ and in picture 2 you have $a=2t+1.$

What are you trying to prove using picture 2?

 

[BvU]

is there any false integrating that i do?

Yes: you treat $v$ as a constant that does not depend on $t$.
$$\int \sqrt{4v+1} \, dt = \int \sqrt{4\,{\bf \color {red} v(t)+1} } \, dt$$

$\$

 

[Kalarudra]

The same answer as what?

Picture 1 and picture 2 are completely different. In picture 1 you have $a=\dfrac{dv}{dt}=g-\kappa v$ and in picture 2 you have $a=2t+1.$

What are you trying to prove using picture 2?

The "answer" That i mean is result of integrating function acceleration with respect to v. I didnt understand why after integrating the function of acceleration with respect to v left side and right side isnt same

 

[erobz]

If you say those two equations are equal ( they both equal $a$) than equate them and solve for $v$. Do you get what you expect for $v$? If you answer “”no” you have done “”false integrating and/or equating of the relationship for $a$”

You’re turned around to the point that it’s difficult to aid you until you explain what you are actually after in words as far as the problem you are trying to solve is concerned. What is the problem you are trying to solve. How do you come to those unrelated equations for $a$?

 

[Demystifier]

Kalarudra, in Fig. 1 you have the differential equation
$$\frac{dv(t)}{dt}=g-\kappa v(t)$$
Assuming the initial condition $v(0)=0$, the solution of this equation is
$$v(t)=\frac{g}{\kappa}(1-e^{-\kappa t})$$
Hence
$$s(t)=\int_0^t v(t) dt = \frac{g}{\kappa} \left( t + \frac{e^{-\kappa t}}{\kappa} - \frac{1}{\kappa} \right)$$
Now you can use this function $s(t)$ to test the result in Fig. 1.