Help me understand a homework solution - intro to ring theory - ideals

[General_Sax]

Help me understand a homework solution -- intro to ring theory -- ideals

problem:

Determine all ideals of Z/Z10.

solution:

the solution is continued on

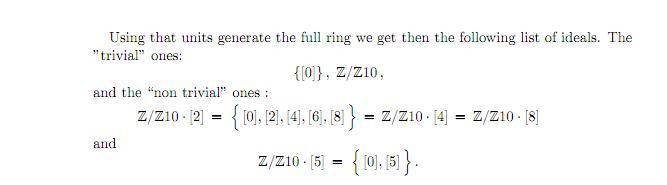
The first paragraph is just saying the ideals generated by the units in the ring is the whole ring correct?

Also, the principal ideals generated by 2, 4 and 8 are all the same correct? So those are three ideals or just one?
So, in the final answer there are 4 ideals in total right?


And finally why do we care about Ideals so much? What use do they even have besides giving students of average intelligence a giant headache in intro abstract algebra course lol?

 

[Deveno]

for any ring, R, if u is a unit, then there is a in R such that au = ua = 1.

this means that 1 is in (u), and since 1 generates R, (u) = R.

it's easy to explicitly calculate ([2]), ([4]) and ([8]).

simply multiply everything in Z₁₀ by [2], if the result is a subgroup of Z₁₀, then that's all there is. (the fact that Z₁₀ is commutative is a big help, here).

so [2](Z₁₀) = {[0],[2],[4],[6],[8]}

([2][5] = [0], [2][6] = [2], [2][7] = [4], [2][8] = [6], [2][9] = [8]).

similarly, [4](Z₁₀ ) = {[0],[4],[8],[2],[6]}, which is clearly the same as ([2]).

the solution given missed one possibility: ([6]), which is the same as ([2]).

note that if k = 2,4,6,8; gcd(k,10) = 2.

why do we care about ideals? well, ideals are ring homomorphism kernels, so they represent things we can "mod out by", and obtain a simpler ring, which shares many of the interesting properties of the original ring, but may be lots easier to deal with. when given any kind of algebraic object A, one main strategy is to describe A in terms of smaller, easier-to-understand sub-objects, and also, to be able to "rebuild A" from knowing the sub-objects (although the latter part turns out to be "too optimistic", we can't always go both ways). certain patterns appear over and over in various structures:

set---------------equivalence relation-------partition
group-----------(normal) subgroup-------quotient group
ring--------------------ideal--------------quotient ring
vector space ---------nullspace---------image space
topological space ----quotient map-------quotient space

the thing at the "end" is what we get via the thing in the "middle", which represents some process of identification (equating things that aren't actually equal).

 

[General_Sax]

Thanks. I appreciate it.