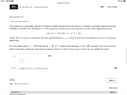
SUMMARY
The discussion centers on solving the equation y = A sin(2*10^6 (π/3 - πt) + φ) to determine the time (t) for a signal to travel a distance of 1.0 x 10^6 m. The relevant formula for signal strength is s(x, t) = A sin(k · x - ω · t + φ), but the primary focus is on calculating time using the formula time = distance/speed. The key challenge is to ascertain the wave speed (v) from the provided data to find the required time.
PREREQUISITES
- Understanding of wave equations and trigonometric functions
- Familiarity with the concepts of wave speed and signal propagation
- Knowledge of the relationship between distance, speed, and time
- Basic proficiency in mathematical manipulation of equations
NEXT STEPS
- Research wave speed calculations in different mediums
- Study the derivation and application of the wave equation s(x, t) = A sin(k · x - ω · t + φ)
- Explore the implications of phase shift (φ) in wave equations
- Learn about the relationship between frequency, wavelength, and wave speed
USEFUL FOR
Students and professionals in physics, engineering, and applied mathematics who are working with wave mechanics and signal analysis will benefit from this discussion.