- #1
Dawei
- 30
- 0
I'm an engineering major taking an advanced level physics class. I realize that I really have no clue when it comes to basic mathematics, and it is extremely frustrating. I always just learned *how* to solve equations, never what I was actually doing.
For example the del operator. What exactly does this mean?
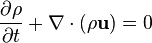
And what is the logic for turning it into this?
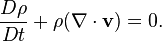
I feel like I just really need a good lesson starting with the very basics. I have no "feel" for what half of the symbols that I'm using mean.
I need to really understand and use the Navier Stokes equations for my job, and it's just killing me. Every time I try to look up a word or symbol I don't know, the explanation of it ends up having like 3 or 4 more words or symbols in it that I don't know. I took calc 1-3 and diff eq, did well in the classes, so it's extremely frustrating now to feel like I never actually learned anything, just sort of how to find patterns and solve homework problems...
Can anyone recommend a good explanation of the Navier Stokes equations for me?
For example the del operator. What exactly does this mean?
And what is the logic for turning it into this?
I feel like I just really need a good lesson starting with the very basics. I have no "feel" for what half of the symbols that I'm using mean.
I need to really understand and use the Navier Stokes equations for my job, and it's just killing me. Every time I try to look up a word or symbol I don't know, the explanation of it ends up having like 3 or 4 more words or symbols in it that I don't know. I took calc 1-3 and diff eq, did well in the classes, so it's extremely frustrating now to feel like I never actually learned anything, just sort of how to find patterns and solve homework problems...
Can anyone recommend a good explanation of the Navier Stokes equations for me?