- #1
Bensky
- 82
- 0
Help with force vectors problem :(
The scale in Fig. P12 is being pulled on via three ropes. (The force on each rope is F = 230 N.) What net force does the scale read?
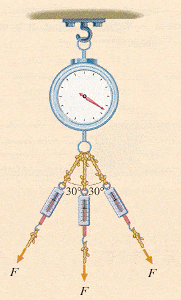
^Fig. P12
Frx = f1x + f2x + f3x
Fry = F1y + f2y + f3y
a^2+b^2=c^2
F = ma (not needed to solve though)
N = Newtons
F1x = -(cos30[tex]\circ[/tex] * 230)
F1x = -199.185 N
F1y = -(sin(30[tex]\circ[/tex] * 230)
F1y = -115 N
F2y = -sin(0[tex]\circ[/tex] * 230)
F2y = -230N
F3x = cos30[tex]\circ[/tex] * 230)
F3x = 199.185 N
F3y = -(sin30[tex]\circ[/tex] * 230)
F3y = -115 N
Frx = -199.185 + 0 + 199.185
Frx = 0
Fry = -115 + -230 + -115
Fry = -460 N
---------------------------
a^2 + b^2 = c^2
0^2 + (-460)^2 = c^2
c = 460 N
(done)
Ok, so the problem is with F2y. I think I might have screwed up since it's facing down - I was thinking about the unit circle and realized that its at a 270 degree angle, not a 0 degree angle. I have one last chance to get this problem right, so I thought I would ask here. Is the angle where I screwed up or did I mess up somewhere else? >_<
Any help is appriciated, thanks.
-Bensky
Homework Statement
The scale in Fig. P12 is being pulled on via three ropes. (The force on each rope is F = 230 N.) What net force does the scale read?
^Fig. P12
Homework Equations
Frx = f1x + f2x + f3x
Fry = F1y + f2y + f3y
a^2+b^2=c^2
F = ma (not needed to solve though)
The Attempt at a Solution
N = Newtons
F1x = -(cos30[tex]\circ[/tex] * 230)
F1x = -199.185 N
F1y = -(sin(30[tex]\circ[/tex] * 230)
F1y = -115 N
F2y = -sin(0[tex]\circ[/tex] * 230)
F2y = -230N
F3x = cos30[tex]\circ[/tex] * 230)
F3x = 199.185 N
F3y = -(sin30[tex]\circ[/tex] * 230)
F3y = -115 N
Frx = -199.185 + 0 + 199.185
Frx = 0
Fry = -115 + -230 + -115
Fry = -460 N
---------------------------
a^2 + b^2 = c^2
0^2 + (-460)^2 = c^2
c = 460 N
(done)
Ok, so the problem is with F2y. I think I might have screwed up since it's facing down - I was thinking about the unit circle and realized that its at a 270 degree angle, not a 0 degree angle. I have one last chance to get this problem right, so I thought I would ask here. Is the angle where I screwed up or did I mess up somewhere else? >_<
Any help is appriciated, thanks.
-Bensky
Last edited: