macardoso
- 4
- 1
- TL;DR
- Working engineer trying to relearn some control theory. Help me understand the derivation for the Inverted Pendulum on a Cart Equations of Motion
Hi All,
My goal is to relearn some control theory and implement a working inverted pendulum on a cart with an industrial linear motor. See video:
Working through an example of an inverted pendulum on a cart posted here: https://ctms.engin.umich.edu/CTMS/index.php?example=InvertedPendulum§ion=SystemModeling
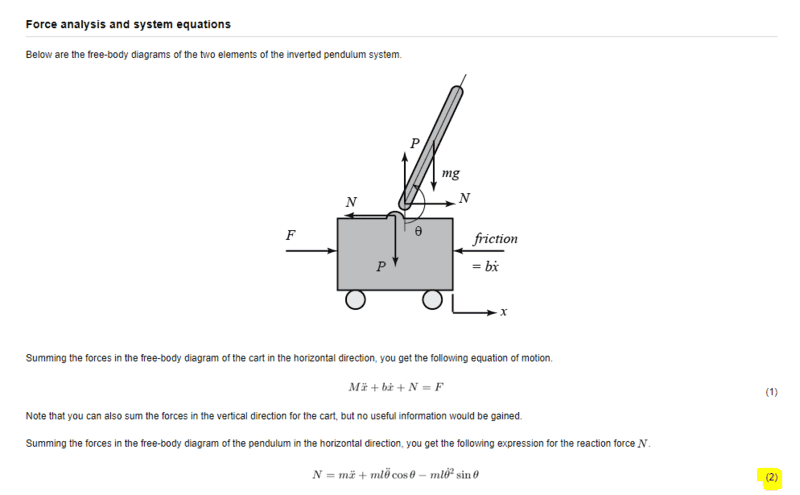
I'm on the part where the pendulum on a cart is broken into free body diagrams and the equations of motion are derived. In the equation below, the horizontal forces on the pendulum are summed to create an equality to the reaction force at the pendulum pivot "N".
When I'm looking at the "Force analysis and system equations", I am trying to understand where all the components of equation (2) come from. I know this is probably elementary, however I am missing some of the steps that are likely glossed over in this example. The equation is:
N = m*x'' + m*L*theta''*cos(theta) - m*L*(theta')^2*sin(theta)
OK, so I understand why "N" is here, it is the horizontal reaction force at the pivot.
m*X'' also makes sense as this is the force felt by the pendulum due to any horizontal acceleration of the system.
I don't understand the term m*L*theta''*cos(theta). I think this might be a torque due to rotational acceleration of the pendulum, but if so, where is the inertia of the rigid body accounted for?
I'm rather unclear about this one, but I have a feeling that m*L*(theta')^2*sin(theta) comes from centripetal acceleration in the form F=m*r*(theta')^2.
I guess one additional question I have is how we know we have actually accounted for all the forces. In this example, I know the end solution so it was easy to see when I was missing something, but if I didn't how would I know if I forgot the centripetal acceleration?
My goal is to relearn some control theory and implement a working inverted pendulum on a cart with an industrial linear motor. See video:
Working through an example of an inverted pendulum on a cart posted here: https://ctms.engin.umich.edu/CTMS/index.php?example=InvertedPendulum§ion=SystemModeling
I'm on the part where the pendulum on a cart is broken into free body diagrams and the equations of motion are derived. In the equation below, the horizontal forces on the pendulum are summed to create an equality to the reaction force at the pendulum pivot "N".
When I'm looking at the "Force analysis and system equations", I am trying to understand where all the components of equation (2) come from. I know this is probably elementary, however I am missing some of the steps that are likely glossed over in this example. The equation is:
N = m*x'' + m*L*theta''*cos(theta) - m*L*(theta')^2*sin(theta)
OK, so I understand why "N" is here, it is the horizontal reaction force at the pivot.
m*X'' also makes sense as this is the force felt by the pendulum due to any horizontal acceleration of the system.
I don't understand the term m*L*theta''*cos(theta). I think this might be a torque due to rotational acceleration of the pendulum, but if so, where is the inertia of the rigid body accounted for?
I'm rather unclear about this one, but I have a feeling that m*L*(theta')^2*sin(theta) comes from centripetal acceleration in the form F=m*r*(theta')^2.
I guess one additional question I have is how we know we have actually accounted for all the forces. In this example, I know the end solution so it was easy to see when I was missing something, but if I didn't how would I know if I forgot the centripetal acceleration?