Discussion Overview
The discussion revolves around the material selection process for a shaft in a hand winch design. Participants explore the implications of stress, deflection, and potential failure modes related to material properties and structural integrity.
Discussion Character
- Technical explanation
- Debate/contested
- Experimental/applied
Main Points Raised
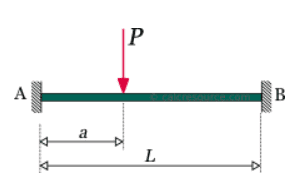
- One participant calculates the maximum stress on the shaft due to bending and questions how to choose a material based on this stress.
- Another participant suggests checking deflection in addition to comparing maximum stress with yield strength.
- A later reply raises questions about the operational conditions of the shaft, such as rotation and axial forces.
- One participant clarifies that the shaft does not rotate and describes the specific application involving a hand winch with an activated brake.
- Another participant warns about the potential for failure due to external compression on the drum, emphasizing the need for a hollow tube design and questioning the required wall thickness.
- One participant shares insights from a disassembled winch, noting the presence of a second hollow tube and a bolt for structural integrity.
- Concerns are raised about whether external compression would significantly impact the design, with one participant asserting it is more significant than deflection.
- Participants discuss the calculation of compressive forces based on rope tension and the number of turns on the drum, with a focus on how these forces contribute to hoop stress.
Areas of Agreement / Disagreement
Participants express differing views on the significance of external compression versus deflection, and there is no consensus on the extent of the impact of these forces on the design. The discussion remains unresolved regarding the specific material selection criteria and the implications of the calculated forces.
Contextual Notes
Participants have not fully explored the assumptions related to material properties, loading conditions, and the specific design constraints of the winch. The discussion includes various calculations and considerations that may depend on additional context or definitions.