Heun's Method for Second Order ODE (Eng Maths)

[jisbon]

Homework Statement

-

Relevant Equations

-

Question:

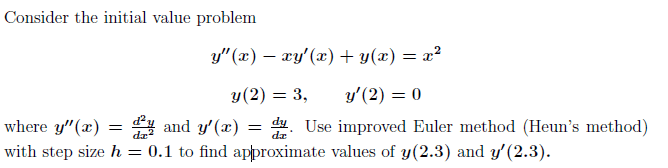
So I got around on doing this example, and I'm pretty sure I messed up somewhere, would appreciate if someone could point out what I did wrongly.
1) For any second ODE, I should let:
$y_{1}= y$ and $y_{2}= y'$
Hence,
$y_{1}'= y' = y_{2}$ and $y_{2}'= y'' = xy(x)+x^2-y(x) = xy_{1}+x^2-y_{1}$
Thus I have 2 functions:
$f_{1}(x,y_{1},y_{2}) = y_{2}$ and$f_{2}(x,y_{1},y_{2}) = xy_{1}+x^2-y_{1}$

Heun's method then states that:

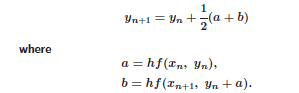I will assume I have to do out a and b for both functions?

 

[pasmith]

Yes.
$$\begin{align*} a_i &= hf_i(x_n,y_{1n}, y_{2n}) \\ b_i &= hf_i(x_{n+1}, y_{1n} + a_1, y_{2n} + a_2) \end{align*}$$