How Does Satellite Mass Impact Velocity Change for Circular Orbit Achievement?

[RiotRick]

Homework Statement

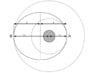
Consider an elliptical orbit of a satellite (of mass m)
around the Earth (of mass M >> m). The perigee is at $r_A$ and the apogee at $r_B$, as measured
from the centre of the Earth, itself located at one of the focal points of the ellipse (see Fig. 1).
We work in an Earth-centered inertial reference frame.

When at apogee, the satellite is given a kick to increase its speed, for instance by burning
fuel and ejecting propellant. Assuming that the kick is instantaneous, by how much should
its speed increase so that the satellite achieves a circular orbit at $r_B$? Does that $\Delta v$ depend
on the satellite’s mass? Qualitatively (without making any precise calculations), does the
amount of fuel burned to achieve the $\Delta v$ depend on the mass? Justify your answer

Homework Equations

delta v from Hohmann transfer orbits

The Attempt at a Solution

I'm a bit confused about the mass.
In the formula is no mass given, so it doesn't depend on "m" but I can't justify the answer. It doesn't make sense to me. If I change the orbit, I'll change the angular momentum. The conservation of angular momentum no longer holds. That means I have to apply torque. Torque is defined as $r \times F$ but F depends on "m". My technical intuition also tells me it should depend on "m".

 

[Orodruin]

Your intuition is wrong. As long as m << M the orbital parameters are all mass independent. This does not mean that you will need the same force/torque as that is mass dependent.

 

[RiotRick]

But at least the amount of fuel does depend on the mass or ist that also wrong?

 

[Orodruin]

But at least the amount of fuel does depend on the mass or ist that also wrong?

Yes, because it takes more energy to give a heavier object the same change in velocity.

 

[RiotRick]

Is my estimation for $\Delta v$ plausible? It already reaches the higher $r_b$ but can't stay on it and get pulled back to the lower $r_A$. So to stay on the higher orbit in a circular orbit $\Delta v$ is around $\sqrt(2*G*\frac{M}{r_B}) - \sqrt(2*G*\frac{M}{r_a})$ from $v=\sqrt(2*G*\frac{M}{r}$

 

[Janus]

It looks like you are trying to use the equation for escape velocity instead of that for orbital velocity. And even if you use orbital velocity, this will not give a good estimate.
As far as working with angular momentum is concerned: Yes, you are changing the orbit, so while the angular momentum for the elliptical orbit is constant, the new orbit will have a new angular momentum. If you consider what the angular momentum is in terms of rmv, what's the difference between the angular momentum of the old orbit vs. the new one and how does this translate into a difference of v at r_a, given that m is a constant?