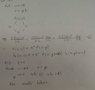Homogeneous function of degree n
- Thread starter athrun200
- Start date
-
- Tags
- Degree Function Homogeneous
Click For Summary
Homogeneous functions of degree n are mathematical functions that exhibit a specific scaling property, where scaling the input by a factor results in the output being scaled by a power of that factor. The discussion revolves around understanding these functions in the context of partial differential equations. The user has successfully solved part a of the homework but is struggling with part b, which requires proving that the mixed partial derivatives f_{xy} and f_{yx} are equal. There is a concern that the problem statement lacks sufficient equations to complete this proof. Clarification on the properties of homogeneous functions and their derivatives is needed to assist in solving part b.