Homology Groups of the Klein Bottle

[Math Amateur]

I am reading James Munkres' book, Elements of Algebraic Topology.

Theorem 6.3 on page 37 concerns the homology groups of the Klein Bottle.

Theorem 6.3 demonstrates that the homology groups for the Klein Bottle are as follows:

H_1 (S) = \mathbb{Z} \oplus \mathbb{Z}/2

and

H_2 (S) = 0

I need some help following a key part of the proof.

The relevant section of the proof is as follows:

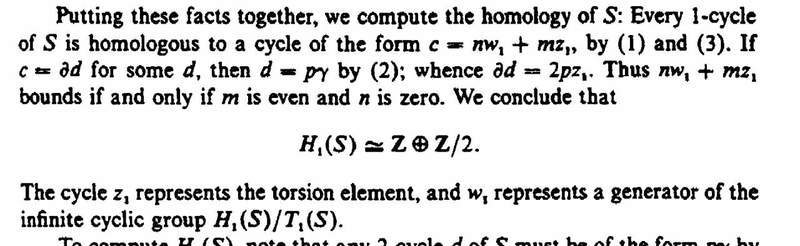
(To provide context to this post, the full theorem and proof is given at the end of this post - see below)

My understanding of the above part of Munkres' proof is as follows:

Munkres establishes that a cycles in S are of the form

c = n w_1 + m z_1

so that Z_1 (S) = \mathbb{Z} \oplus \mathbb{Z}

Munkres also establishes that boundaries are of the form

c = (2p) z_1

so that B_1 (S) = 2 \mathbb{Z}

Thus, so far as I can see we then have:

H_1 (S) = Z_1(S) / B_1 (S) = \mathbb{Z} \oplus \mathbb{Z}/ 2 \mathbb{Z}

BUT ... how does this tally with Munkres expression

H_1 (S) = \mathbb{Z} \oplus \mathbb{Z}/2?

Indeed what does \mathbb{Z} \oplus \mathbb{Z}/2 mean?

(I am not even sure whether the expression is

H_1 (S) = ( \mathbb{Z} \oplus \mathbb{Z}) /2

or

H_1 (S) = \mathbb{Z} \oplus (\mathbb{Z}/2)

Hope someone can help.

The full text of Theorem 6.3 and its proof are as follows:

Hope someone can help.

Peter

 

[WWGD]

For one thing, the quotient $\mathbb Z / \mathbb 2Z$ is isomomorphic to the group $\mathbb Z/2$, and the expression $\mathbb Z (+) \mathbb Z/2$ is the direct sum of rings/modules.