valeriex0x
- 43
- 0
Homework Statement
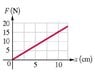
A student measures the force required to stretch a spring by various amounts and makes the graph shown in the figure, which plots this force as a function of the distance the spring has stretched.
Part A) Does this spring obey Hooke's Law?
Part B) What is the force constant of the spring in N/m?
Part C) What force would be needed to stretch the spring a distance of 17 cm from its unstretched length, assuming that it continues to obey Hooke's Law (F=N)?
Homework Equations
F is proportional to displacement x
F=-kx
k=delta f/delta x
The Attempt at a Solution
We didnt cover this in class yet, but I know that a hookean body gets displaced, and once the force is removed it goes back to its original position. Which means that the displacement along the x-axis is the same as the force applied to it.
For part A) I would say No, the spring does not obey Hooke's Law.
For part B) I get -1/2 N/m from F=-kx 5=(-x) 2.5
For part C) -17N from F=(-k ) 17cm