cde42003
- 22
- 0
Can anyone give me some clues as how to do this problem. I have been on it for ever and am stumped. Any help greatly appreciated. Thanks
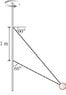
Two wires are tied to the 2.0 kg sphere shown in the figure . The sphere revolves in a horizontal circle at constant speed.
For what speed is the tension the same in both wires?(in m/s)
What is the tension?
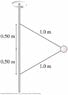
Two wires are tied to the 2.0 kg sphere shown in the figure . The sphere revolves in a horizontal circle at constant speed.
For what speed is the tension the same in both wires?(in m/s)
What is the tension?