How can Castigliano's Method be used to solve for deflections in a cranked beam?

[tlangdon12]

Hello all

I have a beam bending problem I need some help on.

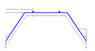
I need to calcuate the deflections at the load (and in the plane of the load) for a simply supported beam with equal point loads overhanging the supports. However my beam is cranked as shown in the attached diagram of the problem geometry.

I know that for a straight beam the formula for the deflection (y) at the loads is

y = Fc²(2c +3b) / 6 EI

where

F = the force applied at each overhang
c = the distance of the overhang
b = the distance between the support
E = the modulus of elasticity of the beam
I = the second area of moment of the beam

(A diagram of the straight beam case is also attached).

Can anyone help me get started on solving this problem?

Thanks

Tony

 

[archis]

I see there are many posts asking to calculate deflections. The problem is it is very hard to explain these calculation theories, algorithms and the calculations take a long time. I recommend to find some building mechanic book to learn or to try search names:
1) Enrico Betti theorem
2) Clapeyron theorem
3) Vereschagin's rule
4) Simpsons rule

 

[racerv]

Anytime i see something start to get complicated i just use Castiglianos's Method. http://www.roymech.co.uk/Useful_Tables/Beams/Beam_energy_methods.html
If you were using this method you would differentiate with respect to the force to get the displacement in that direction (say the y direction). For the x direction you just put a force in there so that you can differentiate w.r.t. that force and once you have the equation you set that imaginary force = 0.