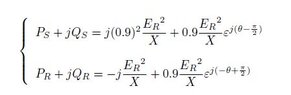How can I find the center and radius of a circle from two different equations?
Click For Summary
SUMMARY
The discussion focuses on determining the center and radius of a circle represented by the equation \(P + Q = K[(0.9)^2j + 0.9e^{j\alpha}]\). The center of the circle is established at the point \((0.9)^2Kj\) and the radius is defined as \(0.9K\). The transformation of the equation into a standard form reveals the geometric properties of the circle in the complex plane, specifically utilizing the exponential function \(e^{j\alpha} = \cos(\alpha) + j \sin(\alpha)\) for simplification.
PREREQUISITES- Understanding of complex numbers, specifically in the form \(Z = X + iY\)
- Familiarity with exponential functions and their properties
- Knowledge of trigonometric identities, particularly sine and cosine
- Basic skills in algebraic manipulation of equations
- Study the properties of circles in the complex plane
- Learn about the geometric interpretation of complex functions
- Explore the relationship between polar and rectangular coordinates
- Investigate the applications of exponential functions in engineering contexts
Mathematicians, engineers, and students studying complex analysis or electrical engineering who need to understand the geometric representation of complex equations and their implications in real-world applications.
Similar threads
- · Replies 2 ·
- · Replies 3 ·
- · Replies 9 ·
- · Replies 5 ·
- · Replies 4 ·
- · Replies 29 ·
High School
Dimension of subset containing two circles
- · Replies 4 ·
- · Replies 3 ·
- · Replies 6 ·
- · Replies 2 ·