Yankel
- 390
- 0
Dear all,
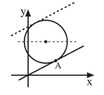
Attached is a picture of a circle.
View attachment 9133
The lower tangent line is y=0.5x. The center of the circle is M(4,7) while the point A is (3,6).
I found the equation of the circle, it is:
$(x-4)^{2}+(y-7)^{2}=20$
and I wish to find the dotted tangent line. I know that it is parallel to the lower one, therefore, the slope is the same. I can't find the tangent point.
Can you give me a hint please ?
Attached is a picture of a circle.
View attachment 9133
The lower tangent line is y=0.5x. The center of the circle is M(4,7) while the point A is (3,6).
I found the equation of the circle, it is:
$(x-4)^{2}+(y-7)^{2}=20$
and I wish to find the dotted tangent line. I know that it is parallel to the lower one, therefore, the slope is the same. I can't find the tangent point.
Can you give me a hint please ?