- #1
Monoxdifly
MHB
- 284
- 0
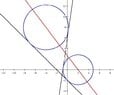
find standard eqations of circles that have centers on 4x+3y=8 and are tangent to both the line x+y=-2 and 7x-y=-6
What I got is \(\displaystyle 4a=–4\pm3r\sqrt2\) and \(\displaystyle b=4\pm r\sqrt2\). Dunno how to continue from here.
What I got is \(\displaystyle 4a=–4\pm3r\sqrt2\) and \(\displaystyle b=4\pm r\sqrt2\). Dunno how to continue from here.