SUMMARY
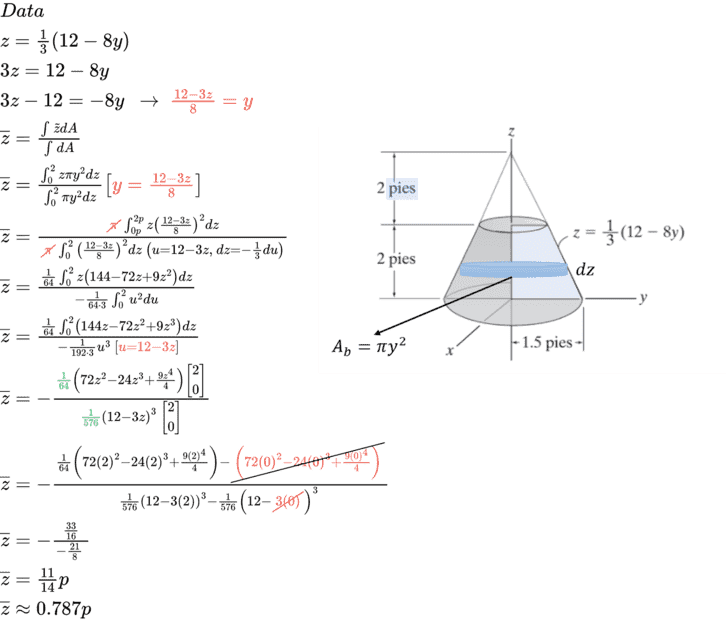
This discussion focuses on locating the coordinates of the centroid of a cone in the Z-axis, specifically addressing the integration limits and the formula for the centroid. The consensus is that the integration should be limited to the range of 0 to 2, as the volume elements above this range do not contribute to the total volume of the shaded region. The simplest formula for the centroid of a cone states that the distance from the base to the centroid is one-fourth the height of the cone. Participants emphasized the importance of understanding the mass center concept and how to apply it to composite shapes.
PREREQUISITES
- Understanding of centroid calculations for geometric shapes
- Familiarity with integration techniques in calculus
- Knowledge of the formula for the centroid of a cone
- Basic principles of center of mass for composite objects
NEXT STEPS
- Study the derivation of the centroid formula for a cone
- Learn about integration limits in volume calculations
- Explore examples of composite shapes and their centroids
- Review video tutorials on calculating centroids and center of mass
USEFUL FOR
Students in engineering and physics, educators teaching calculus and geometry, and anyone interested in understanding centroid calculations for conical shapes.