Discussion Overview
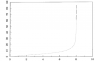
The discussion revolves around finding an equation that approximates a specific graph for use in a toy model. Participants explore various mathematical functions and software tools to generate a suitable fit for the curve depicted in the graph.
Discussion Character
- Exploratory
- Technical explanation
- Mathematical reasoning
Main Points Raised
- One participant expresses difficulty in determining an equation for the graph and mentions using Grapher and Excel for plotting points.
- Another suggests using Excel's trend lines to find a best fit equation, although this approach is later deemed ineffective for the specific curve shape.
- A participant proposes that advanced software like Maple may be necessary if the equation is not a simple polynomial, logarithmic, or exponential function.
- One participant suggests a rough fit with the equation y=10/(8-x) but acknowledges its inaccuracy.
- Another participant mentions the need for the curve to start at the origin and approach large values as x approaches 8, sharing a trial-and-error result of y=exp((x/5.5)^4), which they feel may suffice.
- A later reply critiques the fit of y=exp((x/5.5)^4) and suggests that the function should exhibit a vertical asymptote at x=8, proposing y=5.5 ln(8/(8-x)) as a closer approximation.
- One participant shares that they arrived at y=ln(8/(8-x)) while searching for a suitable fit, noting that another participant had already posted the same function.
Areas of Agreement / Disagreement
Participants express various approaches and suggestions for fitting the graph, but there is no consensus on a single best equation. Multiple competing models and methods are discussed without resolution.
Contextual Notes
Participants mention limitations in their available tools, such as lacking access to advanced software like Maple, which may affect their ability to find a more precise fit. The discussion also highlights the challenge of fitting the curve accurately across its entire range.