How do I determine angle equality in this graph?

[Const@ntine]

Okay, this might be a tad silly, but I cam across this graph/picture i my physics textbook, and for the life of me I can't figure out how to connect the two angles. Here, have a look:

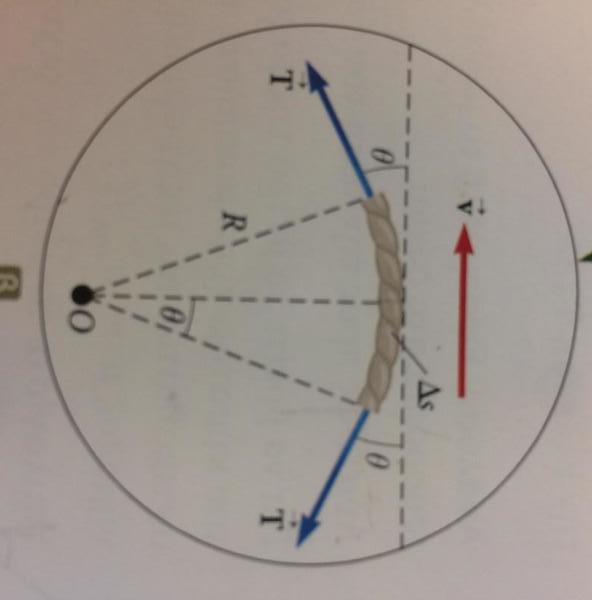
It's not a big part of what the paragraph is about, so in theory I could just skip it, but it's been killing me to not know! Granted, I haven't brushed up on my Trig. for about, what, 3 years now (aside from the basic stuff that I've so far used in First Year Undergrad Physics and Math), so I'm probably missing something.

I tried drawing the "triangles" and trying to find out if there are any opposite/alternate equal angles, but... nothing. The book itself doesn't even mention it beyond the graph, it just takes the equality for granted.

Any kind of help is appreciated!

 

[mfb]

Continue the line where the "R" is until it its the tangent to the circle, then you can relate the two angles via the interior angle sum in the newly generated triangle.

Overall this is one of the standard diagrams to relate angles to each other, but I remember how it is called.

 

[Const@ntine]

Continue the line where the "R" is until it its the tangent to the circle, then you can relate the two angles via the interior angle sum in the newly generated triangle.

Overall this is one of the standard diagrams to relate angles to each other, but I remember how it is called.

Sorry to ask this, but... could you go a bit more in-depth? From what I understand, that's what you're talking about, right?

But I don't see how I can relate the angles of the triangle, and the angle which is created by the "circle" and the tangent.

 

[mfb]

That is the basic diagram, right.

The angle in the upper left corner is $\frac \pi 2 - \theta$ via the angle sum in the large triangle.

Continue the tangent until it reaches the horizontal tangent. Via the angle sum in the small triangle, the angle between the two tangents is $\frac \pi 2 - \left(\frac \pi 2 - \theta\right) = \theta$.

 

[Const@ntine]

That is the basic diagram, right.

The angle in the upper left corner is $\frac \pi 2 - \theta$ via the angle sum in the large triangle.

Continue the tangent until it reaches the horizontal tangent. Via the angle sum in the small triangle, the angle between the two tangents is $\frac \pi 2 - \left(\frac \pi 2 - \theta\right) = \theta$.

Ah, so I draw another tanget, thus creating a smaller triangle, like this:

Yeah, I was focused on just the big triangle and forgot all about the smaller one. Well, that's quite embarassing...

Either way, thanks a ton for the help, twas driving me mad! And I guess I have to brush up on Geometry some time...

 

[mfb]

Here is the diagram at Wikimedia Commons - $\alpha = \beta$.

 

[Const@ntine]

Here is the diagram at Wikimedia Commons - $\alpha = \beta$.

Ah, so that's the general diagram. Thanks (saved)!

The above one (at my RE) is correct for the "matter at hand" though, right?

PS: English isn't my First Language, so there might be some problems when "converting" the info from English to my native one.

 

[mfb]

The above one (at my RE) is correct for the "matter at hand" though, right?

Sure.

PS: English isn't my First Language

Same here.

 

[Const@ntine]

Sure.

Whew, thank goodness!

Same here.

It's a bit of a hurdle, isn't it? I mean, sure, there are special dictionaries for scientific terms, but still.

Either way, thanks a ton for the help!