How can the degrees of freedom of a mechanism be obtained?

[Alfredomaximun]

Summary: $M=3\left(n-1\right)-2j_1-j_2$

Hi, I'm trying to get the degrees of freedom of a can crusher.

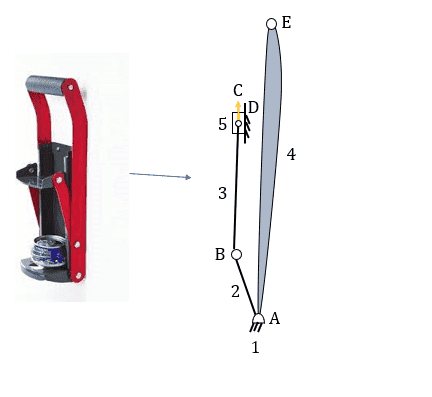
So substituting I get

$\begin{array}{l}M=3\left(n-1\right)-2j_1-j_2\\ n=5\\ j_1=5\\ M=3\left(5-1\right)-2\cdot 5-0\\ M=2\end{array}$

And I would think it would be 1

 

[berkeman]

Welcome to PF.

It's best to define all of your terms when posting equations. Assuming that this is a standard DoF problem, I think:

M = Mobility
n = Number of Links
j = Number of Joints

Is that correct? Also, did you generate the drawing of the can crusher on the right? If so, could you somehow show what corresponds to what on the picture on the left? I'm having trouble seeing how you came up with it.

I agree that I think this crusher "hinge" has basically 1 DoF, but it would be best to understand your drawing first to be sure. Thanks.

https://en.wikipedia.org/wiki/Degrees_of_freedom_(mechanics)

 

[Alfredomaximun]

Bienvenido a PF .

Es mejor definir todos sus términos al publicar ecuaciones. Suponiendo que este es un problema estándar de DoF, creo:

M = movilidad
n = Número de enlaces
j = Número de articulaciones

Es eso correcto? Además, generó el dibujo de la trituradora de la lata a la derecha? Si es así, ¿podría mostrar de alguna manera qué corresponde a qué en la imagen de la izquierda?? Tengo problemas para ver cómo se te ocurrió.

Estoy de acuerdo en que creo que esta "bisagras" de la trituradora tiene básicamente 1 DoF, pero sería mejor entender su dibujo primero para estar seguro. Gracias.

https://en.wikipedia.org/wiki/Degrees_of_freedom_(mecánica)

Hi Berkeman, I changed the image and did it above but it doesn't seem to be correct

The original image was this