- #1
Sanchayan Ghosh
- 11
- 0
Hello guys,
I have a doubt with understanding DOFs. I have taken the example of the four bar linkage. According to Grueblr's condition, the DOF of this mechanism is 1.
[tex]\mbox{DOF} = 3(l-1) + 2j_1 + 2j_2\\l=4\ j_1=4\ j_2=0\\\mbox{DOF} = 1[/tex]
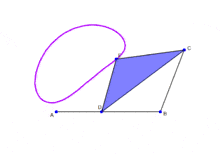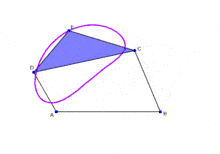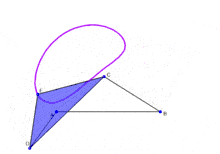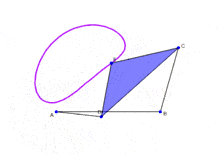
In the above figure, the links next to the ground link rotate. So it should be 2 DOFs. Then, the ternary link rotates, so it should be 1 more DOF. However, it is not so. This is a really fundamental place I am going wrong in. May anyone please explain this, as due to this I have difficulty understanding isomers in mechanisms.
Thank You
I have a doubt with understanding DOFs. I have taken the example of the four bar linkage. According to Grueblr's condition, the DOF of this mechanism is 1.
[tex]\mbox{DOF} = 3(l-1) + 2j_1 + 2j_2\\l=4\ j_1=4\ j_2=0\\\mbox{DOF} = 1[/tex]
In the above figure, the links next to the ground link rotate. So it should be 2 DOFs. Then, the ternary link rotates, so it should be 1 more DOF. However, it is not so. This is a really fundamental place I am going wrong in. May anyone please explain this, as due to this I have difficulty understanding isomers in mechanisms.
Thank You
Last edited by a moderator: