SUMMARY
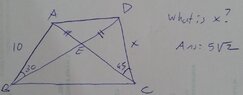
The sine rule, or law of sines, is a critical tool for determining unknown lengths in irregular shapes. In the discussion, participants emphasize its application in solving for the unknown length 'x' in a triangle where angles EAD and EDA are equal. The sine rule states that the ratio of a side length to the sine of its opposite angle is constant across all sides of the triangle. This principle allows for the calculation of missing dimensions when certain angles and sides are known.
PREREQUISITES
- Understanding of basic trigonometry concepts
- Familiarity with the sine rule (law of sines)
- Knowledge of triangle properties, particularly isosceles triangles
- Ability to interpret geometric diagrams
NEXT STEPS
- Study the derivation and applications of the sine rule in various geometric contexts
- Explore advanced trigonometric identities and their uses in irregular shapes
- Learn about the law of cosines for additional triangle calculations
- Practice solving problems involving the sine rule with irregular shapes
USEFUL FOR
Students, educators, and professionals in mathematics, engineering, and architecture who require a deeper understanding of trigonometric applications in irregular geometric shapes.