How can the water level in a trough be calculated using related rates?

Click For Summary
SUMMARY

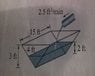
The discussion focuses on calculating the water level in a trough using related rates, specifically for a trough that is 15 feet long and has an isosceles triangular cross-section with a height of 3 feet. The water enters the trough at a rate of 2.5 cubic feet per minute. To determine how fast the water level rises when it is 2 feet deep, participants emphasize the need to calculate the area of the water's surface rather than the volume of the entire triangular prism. The correct approach involves using the formula for the volume of a triangular prism and the relationship between volume and height.

PREREQUISITES
  • Understanding of related rates in calculus
  • Familiarity with the volume formula for triangular prisms
  • Knowledge of how to derive relationships between different geometric dimensions
  • Basic skills in solving differential equations
NEXT STEPS
  • Study the concept of related rates in calculus
  • Learn how to derive the volume of a triangular prism based on varying dimensions
  • Explore examples of similar problems involving water flow and geometric shapes
  • Practice solving differential equations related to volume and height changes
USEFUL FOR

Students studying calculus, particularly those focusing on related rates, as well as educators seeking to explain geometric applications in real-world scenarios.

iRaid
Messages
558
Reaction score
8

Homework Statement


12.) A trough is 15ft long and 4ft across the top as shown in the figure. Its ends are isosceles triangles with height 3ft. Water runs into the trough at the rate of 2.5 ft3/min. How fast is the water level rising when it is 2 ft deep?

Homework Equations


The Attempt at a Solution



Not sure how to do this..
dv/dt = 2.5

I tried using the volume of a triangular prism: V=(1/2)bhl but no success.. I think the problem is IDK which numbers to use for the volume equation?
Can someone point me in the correct direction?
 

Attachments

  • d.jpg
    d.jpg
    6.9 KB · Views: 497
Last edited:
Physics news on Phys.org
Edit: Attached picture
 
If anyone is looking at this, what you have to do is find the area of the water, not the actual triangular prism.
 

Similar threads

How Fast Is the Water Level Rising in a Trough as It Fills?
  • · Replies 1 ·
Replies
1
Views
3K
Related rates (prism with a trapezoid base)
  • · Replies 3 ·
Replies
3
Views
3K
Rate of change of a triangular prisim
  • · Replies 2 ·
Replies
2
Views
1K
Calculating Minimum Water Level in a Barrel using ODE: Analysis and Approach
  • · Replies 3 ·
Replies
3
Views
2K
Finding the Rate of Change of Water Height in a Filling Cylindrical Tank
  • · Replies 11 ·
Replies
11
Views
3K
Isosceles Triangle related rates problem
  • · Replies 5 ·
Replies
5
Views
9K
Isosceles Triangular Prism Related Rates Problem
  • · Replies 8 ·
Replies
8
Views
13K
How to Calculate Water Level Changes in a Filling Trough
  • · Replies 4 ·
Replies
4
Views
2K
Related Rates: Water Trough Volume and Rate of Change
  • · Replies 7 ·
Replies
7
Views
5K
Finding Rate of Change for Water Level in a Trough
  • · Replies 3 ·
Replies
3
Views
5K