DaalChawal said:
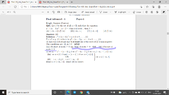
View attachment 11330
I am confused in (iia) and (iib).
If $x^4 +( \alpha - 1) x^2 + \alpha + 2 = 0$ has real roots that means $y^2 + ( \alpha -1) + \alpha + 2 =0 $ should have at least one non-negative root. This means product of roots of (2) can be greater or less than zero...But I'm not able to comment on sum of roots.
Help Please.
Let's assume from here on that the discriminant is $\ge 0$. Otherwise there is no solution.
Now let's forget about roots that can be zero for a moment.
If the product of the roots is positive, then that means that either both roots are positive, or both roots are negative.
Otherwise the product is not positive.
So we can't tell yet if we have at least one positive root.
However, if there is at least one positive, then the other root must also be positive, so their sum must be positive.
And if both roots are negative, then their sum must be negative.
So the sum of the roots allows us to distinguish cases.
In short if $\text{Product of roots} >0 \text{ and } \text{Sum of roots} > 0$, then we have a non-negative root as desired.
If the product of the roots is negative, then that means there is one positive root and one negative root, so we have what we need.
In short if $\text{Product of roots} <0$, then we have a non-negative root as desired.
Now let's go back to roots that could be zero.
If at least one root is zero, then the product is zero as well, and we have a non-negative root as desired.
In short if $\text{Product of roots} =0$, then we have a non-negative root as desired.
In all other cases, we don't have a non-negative root.
Can we combine those 3 conditions into what we have in (iia) and (iib)?