How can you calculate change in magnetic flux?

[michaelw]

Here is the problem

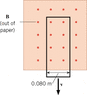
A long and narrow rectangular loop of wire is moving toward the bottom of the page with a speed of 0.020m/s (see the drawing). The loop is leaving a region in which a 2.4-T magnetic field exists; the magnetic field outside this region is zero. During a time of 2.0s, what is the magnitude of the change in the magnetic flux?

Please help me.. how do I do this?

 

[asrodan]

hrm...

Since the magnetic flux is completely perpendicular to the loop, the magnetic flux at anytime is B*A, where A is only the area that is within the magnetic field.

Magnetic flux = B*A you can differentiate this equation with respect to time to find the rate of change of flux, and relate dA/dt to the information given in the question.

Because you are looking for the change only, you do not need to the know the total area, or the length, of the loop.

 

[michaelw]

is there a way to do it without involving calculus :)?

 

[dextercioby]

You can do it,if the velocity is constant...(I think it is).

So yes.

\Delta \Phi =B \Delta A

What is the variation of the area...?

Daniel.

 

[michaelw]

thanks :)
are the units for magnetic flux Tm^2 (the SI unit)

 

[dextercioby]

1 Tm^2 is equal to one 1 Weber.

Daniel.