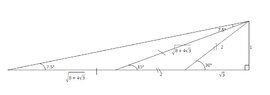
SUMMARY
The discussion centers on proving that $\cot 7.5^{\circ}$ equals the sum of four square roots: $\sqrt{2} + \sqrt{3} + \sqrt{4} + \sqrt{6}$. Participants highlight a geometric approach involving triangle construction to simplify the proof. The method is noted for its clarity and effectiveness, showcasing a visual representation of the mathematical relationship.
PREREQUISITES
- Understanding of trigonometric functions, specifically cotangent.
- Familiarity with geometric principles related to triangles.
- Knowledge of square roots and their properties.
- Basic skills in mathematical proof techniques.
NEXT STEPS
- Explore trigonometric identities and their applications in proofs.
- Study geometric interpretations of trigonometric functions.
- Learn about the properties of square roots in mathematical expressions.
- Investigate advanced proof techniques in trigonometry and geometry.
USEFUL FOR
Mathematicians, students studying trigonometry, educators looking for teaching methods, and anyone interested in geometric proofs.