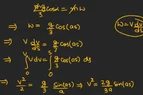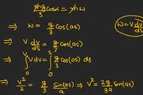How do I derive an expression for the velocity vector for any α?

[griffith]

Homework Statement

This question is part of a homework set. I have shown my attempt and would like help understanding the concepts involved.

Relevant Equations

md2/dt2(s) = Fcos(as)

[Mentor Note: OP's two duplicate thread starts have been merged, and OP has come back and edited the first post to include work]

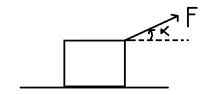
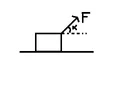
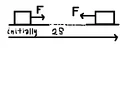
A bar of mass m resting on a smooth horizontal plane starts
moving due to the force F of constant magnitude. In the
process of its rectilinear motion the angle α between the direction of
this force and the horizontal varies as α = as, where a is a constant,
and s is the distance traversed by the bar from its initial position.
Find the velocity vector of the bar as a function of the angle α. I have tried solving it for all α in the interval [0, inf] but I was only able to find the velocity vector for the angle α in the interval [0,pi/2].

 

[griffith]

A bar of mass m resting on a smooth horizontal plane starts moving due to the force F of constant magnitude. In the process of its rectilinear motion the angle α between the direction of this force and the horizontal varies as α = as, where a is a constant, and s is the distance traversed by the bar from its initial position. Find the velocity vector of the bar as a function of the angle α.

[Mentor Note: New user has been reminded to always show their work when posting schoolwork questions at PF.]

 

[wrobel]

picture is needed

 

[griffith]

picture is needed

Sure, a sec

 

[jedishrfu]

Please read our site guidelines regarding homework requests.

We do not provide answers, only hints.

But here's the big one: You must show some work before we post anything.

 

[griffith]

picture is needed

 

[wrobel]

the 2nd Newton is $m\ddot s=F\cos(as)$ and $s(0)=0,\quad \dot s(0)=0$.
multiply both sides of the equation by $\dot s$:
$m\ddot s\dot s=F\dot s\cos(as)$ or equivalently
$$\frac{d}{dt}\Big(\frac{1}{2}m\dot s^2-\frac{F}{a}\sin(as)\Big)=0$$
finish it by yourself

 

[griffith]

the 2nd Newton is $m\ddot s=F\cos(as)$ and $s(0)=0,\quad \dot s(0)=0$.
multiply both sides of the equation by $\dot s$:
$m\ddot s\dot s=F\dot s\cos(as)$ or equivalently
$$\frac{d}{dt}\Big(\frac{1}{2}m\dot s^2-\frac{F}{a}\sin(as)\Big)=0$$
finish it by yourself

Could you clarify why the final result is only valid over a limited range of α, and what prevents extending it to all α

 

[wrobel]

You ask irrelevant question. Analyze formulas and make sure that $as(t)\in [0,\pi]$ for all $t\ge 0$;
$s(t)$ is a periodic function

 

[griffith]

the 2nd Newton is $m\ddot s=F\cos(as)$ and $s(0)=0,\quad \dot s(0)=0$.
multiply both sides of the equation by $\dot s$:
$m\ddot s\dot s=F\dot s\cos(as)$ or equivalently
$$\frac{d}{dt}\Big(\frac{1}{2}m\dot s^2-\frac{F}{a}\sin(as)\Big)=0$$
finish it by yourself

my doubt was stupid. that time derivative when simplified gives:
1/2m.(ds/dt)^2 = (F/a).sin(as)
-----> ds/dt = +-[(2F/ma).sin(as)]^1/2
since ds/dt > 0 , ds/dt = [(2F/ma).sin(as)]^1/2
the body accelerates from as----->0 to pi/2 , attains maximum speed(say at distance S from the initial point) and retards at the same rate i.e., its velocity is equal to 0 at distance 2S from the initial point. At that distance 2S from the initial point it just repeats everything it has done in the opposite sense (motion towards the initial point). I finally get it now

 

[vela]

Find the velocity vector of the bar as a function of the angle α. I have tried solving it for all α in the interval [0, inf] but I was only able to find the velocity vector for the angle α in the interval [0,pi/2].

I assume you're troubled by the fact that when $\alpha > \pi$, the expression you derived gives you $v^2<0$.

When $\alpha = \pi$, what's the velocity of the bar and which way does the force point?

 

[griffith]

I assume you're troubled by the fact that when $\alpha > \pi$, the expression you derived gives you $v^2<0$.

When $\alpha = \pi$, what's the velocity of the bar and which way does the force point?

velocity equals 0 and the force vector would point to the left(wrt the pic i drew)

 

[haruspex]

velocity equals 0 and the force vector would point to the left(wrt the pic i drew)

And at that point, $s=\pi/\alpha$. When will $s$ exceed that?

 

[wrobel]

Actually it is a pendulum. The equations of motion are the same as ones for the pendulum.

 

[Gavran]

I have tried solving it for all α in the interval [0, inf] but I was only able to find the velocity vector for the angle α in the interval [0,pi/2].

This is a periodic back-and-forth motion, and $s$ is the distance of the moving bar from its initial position. Why do you expect $s=\alpha/a$ to be in the interval $[0,\infty)$?

 

[griffith]

And at that point, $s=\pi/\alpha$. When will $s$ exceed that?

s belongs to the interval [0, pi/a]

 

[griffith]

This is a periodic back-and-forth motion, and $s$ is the distance of the moving bar from its initial position. Why do you expect $s=\alpha/a$ to be in the interval $[0,\infty)$?

It's because I misinterpreted the line "s is the distance traversed by the bar from its initial position"

 

[griffith]

Actually it is a pendulum. The equations of motion are the same as ones for the pendulum.

what if s is the total distance traversed by the body?

 

[wrobel]

the equation of motion has already been written what else do you want ?

 

[griffith]

the equation of motion has already been written what else do you want ?

that only works if s is the magnitude of displacement. How would one proceed if s is taken to be the total distance traveled along the path,
Also, why wasn’t s taken as the modulus of the displacement vector?
Is this because, from the analysis of the motion, the body never crosses the initial point in the opposite sense?

 

[wrobel]

it is hard to answer questions that contain incorrect prerequisites in their formulations

:)

 

[PeroK]

that only works if s is the magnitude of displacement. How would one proceed if s is taken to be the total distance traveled along the path,
Also, why wasn’t s taken as the modulus of the displacement vector?
Is this because, from the analysis of the motion, the body never crosses the initial point in the opposite sense?

The question is a bit odd. Presumably, the bar does not get lifted off the surface, so that we have an assumed constraint of motion in one direction. In this case, the vertical component of the force is irrelevant. Initially, displacement and distance are the same. They remain the same until the bar starts moving in the opposite direction (if, indeed, that happens).

We have a force that varies with the displacement/distance ($s$) from the starting point, given by:
$$F_s = F\cos(as)$$The will be to the right (assuming $a > 0$) until $as = \frac \pi 2$ and to the left until $as = \pi$. By symmetry, the block will have stopped at that point.

If we take $s$ to be the displacement, then the variable $as$ reduces from that point and we have the cosine of an angle in the second and first quadrants. And we get simple harmonic motion.

If we take $s$ to be the distance, then the variable $as$ continues to increase and we get the same force in the horizontal direction as in the previous case. Although the force in the vertical direction has is downwards, rather than upwards.

It doesn't matter to the cosine function whether $\alpha \in [0, \pi]$ or $\alpha \in [0, \infty)$, in this particular case.

Feynman is supposed to have said "the same equations have the same solutions". This is a case in point. Someone thought it was a good idea to disguise SHM in some slightly physically bizarre scenario with a horizontal bar/block and a weird force. Maybe the student learns something from this and maybe it confuses the student.

I lean towards the latter.

 

[wrobel]

SHM

it is not simple harmonic motion

 

[griffith]

it is hard to answer questions that contain incorrect prerequisites in their formulations

:)

true

 

[griffith]

The question is a bit odd. Presumably, the bar does not get lifted off the surface, so that we have an assumed constraint of motion in one direction. In this case, the vertical component of the force is irrelevant. Initially, displacement and distance are the same. They remain the same until the bar starts moving in the opposite direction (if, indeed, that happens).

We have a force that varies with the displacement/distance ($s$) from the starting point, given by:
$$F_s = F\cos(as)$$The will be to the right (assuming $a > 0$) until $as = \frac \pi 2$ and to the left until $as = \pi$. By symmetry, the block will have stopped at that point.

If we take $s$ to be the displacement, then the variable $as$ reduces from that point and we have the cosine of an angle in the second and first quadrants. And we get simple harmonic motion.

If we take $s$ to be the distance, then the variable $as$ continues to increase and we get the same force in the horizontal direction as in the previous case. Although the force in the vertical direction has is downwards, rather than upwards.

It doesn't matter to the cosine function whether $\alpha \in [0, \pi]$ or $\alpha \in [0, \infty)$, in this particular case.

Feynman is supposed to have said "the same equations have the same solutions". This is a case in point. Someone thought it was a good idea to disguise SHM in some slightly physically bizarre scenario with a horizontal bar/block and a weird force. Maybe the student learns something from this and maybe it confuses the student.

I lean towards the latter.

In the diagram, the arrows attached to each block represent the applied force vector at different positions along the motion.


In case (1), regardless of whether s is interpreted as the displacement from the initial point or as the distance traveled, the resulting motion is the same because the body has not reversed direction.


In case (2), s is naturally interpreted as the displacement from the initial position, whereas in case (3), s represents the total distance traveled along the path.


In either interpretation, however, the horizontal component of the force vector, which governs the rectilinear motion of the body on the smooth plane, remains the same at a given value of the angle. Therefore, the equation of motion along the horizontal direction is unaffected by whether s is taken as displacement or as distance, provided the direction of motion is treated consistently. (Apologies for the rough sketch)

 

[haruspex]

what if s is the total distance traversed by the body?

The exact wording suggests that is the intention. This is reinforced by its asking for the velocity vector, not the speed. If we only take $s$ as the modulus of the displacement then the sign of $v$ is indeterminate.

To avoid confusion, I'll use $S$ for the displacement (which is never negative) and $s$ for the cumulative traversal.
In post #1 you found that $(\dot S)^2=(2F/ma)\sin(aS)$.
You derived this from an equation of the form $\ddot S=k\cos(aS)$.
But if we define $s$ as the cumulative distance then the initial equation for that is different. If we plot $S$ against $s$ we get a sawtooth: /\/\/\… ; $\dot s$ is nonnegative always, but $\dot S$ alternates between $\dot s$ and $-\dot s$.

A solution for $\dot S$ (which the question appears to be asking for) can be written in terms of $s$ by using functions like modulo() and sign(). This is most easily done by starting with the solution for $\dot S$ as a function of $S$ and applying a little reasoning, rather than starting from scratch with the right differential equation.

 

[vela]

what if s is the total distance traversed by the body?

You have
$$a = v \frac{dv}{dx}$$ where $x$ is the displacement. As the block initially moves to the right, you have $x=s$, so the equation you derived works. When the block moves to the left, however, you no longer can say $x=s$, but you can say that $dx = -ds$ which gives you the minus sign you're looking for.