How do I determine the distribution of shear flow along a bent metal?

[lizzyb]

Question
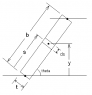
We have a bent piece of metal subjected to a shear V; we're to sketch the distribution of shear flow along the leg AB. (see attached)

What I've Done So Far
I've tried to determine the second moment of inertia but have failed to produce the same results given in the hints. Specifically, I took the neutral axis to be a line directly down the center of the triangle cross section:

http://img182.imageshack.us/img182/1663/scannedimage027.jpg

http://img190.imageshack.us/img190/7893/scannedimage028e.jpg

http://img521.imageshack.us/img521/6183/scannedimage029.jpg

http://img18.imageshack.us/img18/4112/scannedimage030.jpg

Anyway, that failed to produce the answer given in the hints and even then I'm not sure if I'm headed in the right direction to produce Q(x).

 

[nvn]

lizzyb: Bending is not about the vertical axis of your cantilever. The shear force, V, is vertical; therefore, bending is about what axis? Try it again.

 

[lizzyb]

Even if I do it about the X axis I still come up with the wrong answer. What am doing wrong?

http://img169.imageshack.us/img169/3494/scannedimage044.jpg

http://img182.imageshack.us/img182/4513/scannedimage045.jpg

 

[nvn]

The neutral axis should not be at the bottom of the cross section. Try it again.

 

[lizzyb]

Placing the Neutral Axis up 1/3 of the way:

http://img33.imageshack.us/img33/7333/scannedimage047.jpg

http://img245.imageshack.us/img245/214/scannedimage046.jpg

http://img268.imageshack.us/img268/5239/scannedimage048.jpg

http://img31.imageshack.us/img31/1637/scannedimage049.jpg

Its still no good.

 

[nvn]

Good try. But these are not triangles. The cross section consists of two slanted rectangles. Your neutral axis location appears to be incorrect.

 

[lizzyb]

I found the centroid to be at b/2 (or y = b/(2 sqrt(2)) but still come up with the exact same I = (b^3 t)/3.

Another method is to dissect the structure into its component parts but appears way too laborious what with the parallel-axis theorem and all.

 

[nvn]

For now, let's pretend the problem can be treated as a thin section and can be idealized as two identical, rotated rectangles, one of which is shown in the attached file. Based on these assumptions, your current answer for the centroid is correct. But your answer for I is currently incorrect. Try it again; and show your work if you want someone to check your math. Do you have the answer for I in the back of the book?

 

[lizzyb]

I have the value of I and the solution I've been coming up with (b^3 t)/3 is exactly 4 times the given solution which I'm unable to account for. My latest attempt is thus (note that it is not multiplied by 2 and represents a single slanted rectangle; note also that the given solution matches the standard equation of a single rectangle [1/2 * b * h^3]):

http://img404.imageshack.us/img404/4460/scannedimage050.jpg

http://img150.imageshack.us/img150/1686/scannedimage051.jpg

http://img200.imageshack.us/img200/4863/scannedimage052.jpg

The answer was produced with a calculator:

http://img200.imageshack.us/img200/1135/scannedimage053.jpg

 

[nvn]

You must compute the area moment of inertia, I, about the cross section neutral axis. Look at your above equation for y. When you plug in s = 0, do you get y = 0? If not, your y origin is not at the neutral axis. Hint: Any y equation you wish to construct must correspond to the limits of integration you use, or vice versa. Keep trying.

 

[lizzyb]

Yes that's what did it; should help greatly when developing Q. Thank you for your help.

http://img405.imageshack.us/img405/3769/scannedimage057.jpg http://img36.imageshack.us/img36/3262/scannedimage055.jpg http://img190.imageshack.us/img190/8568/scannedimage056.jpg