How do I find refractive index uncertainties?

[Sam D]

I've been doing an experiment where I've used prisms and a spectrometer to find the exact angles inside the prisms and the refractive index of the prisms by finding the minimum angle of deviation.

I have attached a picture of the formula I've been using to find the refractive indices. Where Dmin in the minimum angle of deviation and A is the measurement I've made of the angles in the prism (both of which in themselves have uncertainties).

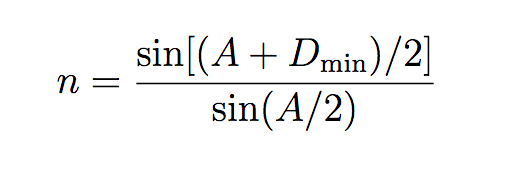
I'm now trying to find the uncertainty in my value for the refractive index but I'm really struggling because there are so many components to go through. I'd be really grateful if someone could talk me through the easiest way of finding the uncertainty in my refractive index values.

Thanks in advance for your help.

 

[DrDu]

This does not look too complicated. The only point I see is that you should use the formula to express the sine of a sum as a sum of products of the trigonometric functions of the individual variables.

 

[Sam D]

I found the uncertainties of A and Dmin, the uncertainty when they're added together and divided by two, the uncertainty of them in sin, the uncertainty of a/2 in sin and then the uncertainty of everything on the top divided by everything on the bottom?

 

[DrDu]

[...]and then the uncertainty of everything on the top divided by everything on the bottom?

That's the problematic point as the uncertainties in the numerator and denominator will be correlated. Rather use error propagation. In the first step, you will have to take derivatives of your expression with respect to A and Dmin.