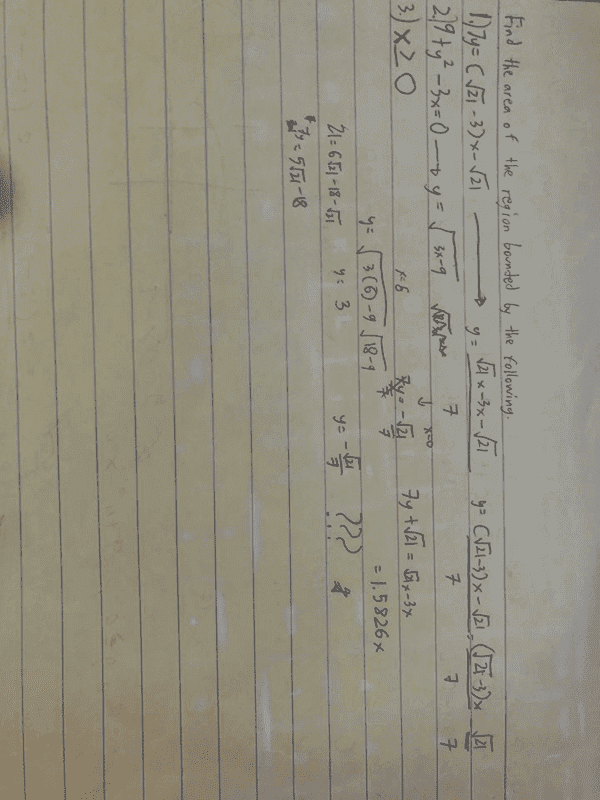SUMMARY
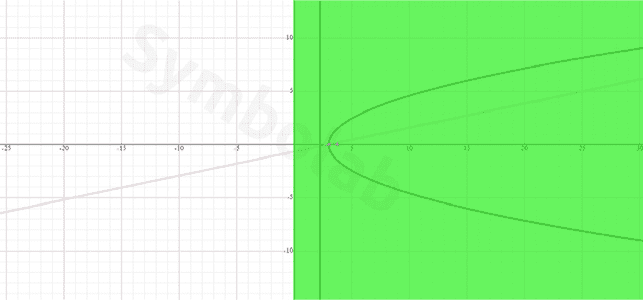
The discussion focuses on finding the area of a region bounded by multiple functions using integrals. Participants emphasize the importance of identifying intersection points of the equations and suggest integrating either over x or y, depending on which setup appears simpler. A key recommendation is to split the area into two regions for easier calculation in certain scenarios. The conversation highlights the necessity of clarity in presenting mathematical approaches and solutions.
PREREQUISITES
- Understanding of integral calculus
- Familiarity with finding intersection points of functions
- Knowledge of setting up definite integrals
- Ability to interpret graphical representations of functions
NEXT STEPS
- Research methods for finding intersection points of equations
- Learn about setting up definite integrals for area calculation
- Explore techniques for splitting regions in integral calculus
- Study graphical interpretation of functions and their boundaries
USEFUL FOR
Students and educators in mathematics, particularly those focusing on calculus and integral applications, as well as anyone involved in solving area-related problems in a multi-variable context.