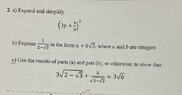SUMMARY
The discussion focuses on solving the equation involving a surd, specifically proving that \( x^2 = 54 \) where \( x = 3\sqrt{2 - \sqrt{3}} + \frac{3}{\sqrt{2 - \sqrt{3}}} \). Participants emphasize that starting with \( = 54 \) is incorrect as it assumes the conclusion. Instead, they recommend simplifying \( x^2 \) step-by-step using algebraic techniques to arrive at the conclusion. The final resolution confirms that \( 54 \) can be expressed as \( 3\sqrt{6} \).
PREREQUISITES
- Understanding of algebraic manipulation
- Familiarity with surds and square roots
- Knowledge of simplification techniques in mathematics
- Ability to work with expressions involving radicals
NEXT STEPS
- Study algebraic identities and their applications in simplifying expressions
- Learn about surd simplification techniques
- Explore the properties of square roots and their implications in equations
- Practice solving equations involving radicals and surds
USEFUL FOR
Students, educators, and anyone interested in mastering algebraic expressions involving surds and radicals.