How do nodes on a string produce tension if they are stationary?

[bob900]

The vibration in a string is caused by the tension force on point masses inside the string :

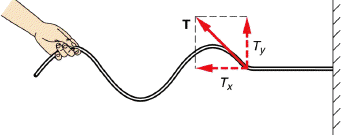
The tension force itself results from "the net electrostatic attraction between the particles in a solid when it is deformed so that the particles are further apart from each other than when at equilibrium" (source).

But a node in the string (when two waves cancel each other) is stationary. To transmit movement to string masses on either side of the node, shouldn't the node have to move (deform) to produce tension?

For example, in the following picture

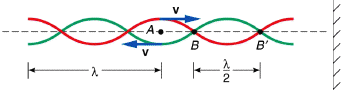
At node B, the red wave traveling to the right, has to create tension to transmit its upward to the string mass immediately to the right of B. Analogously, the green wave has to create tension to transmit its downward movement to the string mass on the left of B. But if the mass element at B itself does not move, how are these tension forces produced?

 

[Studiot]

The rope has to have some tension before you start waggling it.

A completely slack string will not oscillate.

Try it and see.

 

[bob900]

The rope has to have some tension before you start waggling it.

A completely slack string will not oscillate.

Try it and see.

I know that you need tension to start oscillating. What I'm asking is that when it is oscillating already, how is force/tension/anything transmitted through the stationary nodes, if they don't move at all? On a microscopic, electrostatic force level.

 

[Studiot]

What I'm asking is that when it is oscillating already, how is force/tension/anything transmitted through the stationary nodes,

As I indicated a vibrating string is already under tension throughout.

Energy does not pass a node. That is why this type of wave is called a stationary (or standing) wave.

The force of tension is a vector.
The theory of small oscillations assumes the tension does not vary in magnitude along the string, just in direction.

 

[sophiecentaur]

As I indicated a vibrating string is already under tension throughout.

Energy does not pass a node. That is why this type of wave is called a stationary (or standing) wave.

The force of tension is a vector.
The theory of small oscillations assumes the tension does not vary in magnitude along the string, just in direction.

Energy is flowing past each node - it's just that energy is being carried in both directions by two progressive waves, which add up to a standing wave. You need to remember that the (extra) tension in the string varies from zero to a maximum during each half of the oscillation.