How Do We Calculate Surface Charge Density on a Non-Conducting Shell?

[rudransh verma]

Homework Statement

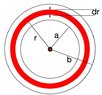
An hollow nonconducting sphere/ shell with a inner radius of a=1.5 cm and outer radius of b=2.4 cm has a volume charge density of rho =A/r and at the center a ball charge of q=+75 fC.
What is the value of A if electric field inside the shell(a<=r<=b) is to be uniform ?

Relevant Equations

In the solution it is establishing a relationship between volume charge density and net charge on sphere.

delta q=rho deltaV
rho=dq/dV
dq=rho4pir^2dr
Then integrate dq from 0 to a because A is to be uniform in shell.

Ans: A= 5.3*10^-11 C/m^2

How do we approach these problems? Looking at the answer A seems to be surface charge density. What is A? What is the direction of uniform field E. I don’t think there will be any movement of charges because it’s non conductor.

 

[haruspex]

Then integrate dq from 0 to a because A is to be uniform in shell

That does not make sense. The charge described by $dq=\rho 4\pi r^2dr$ only exists between r=a and r=b.
I believe it is only the magnitude of the field that is to be uniform in the shell.

At radius r within the shell, what is the total charge "contained" (i.e. at lower radius)? What field does that produce at radius r?

 

[rudransh verma]

At radius r within the shell, what is the total charge "contained" (i.e. at lower radius)? What field does that produce at radius r?

I don’t know. Do you want to see the solution?

 

[haruspex]

I don’t know.

Then figure it out.
If the charge density is $\rho(r)$, how much charge lies between radius a and radius r?

 

[rudransh verma]

by dq=ρ4πr2dr

Integration of this from a to r will give us charge I guess

 

[haruspex]

Integration of this from a to r will give us charge I guess

Yes, so do that, but remember ρ is a function of r.

 

[rudransh verma]

Yes, so do that, but remember ρ is a function of

This is A. But we don’t know r, only a and b .

 

[haruspex]

This is A. But we don’t know r, only a and b .

Your first three equations are good, but next you need to add the isolated charge at the centre to get the total charge contained inside radius r.
Next, write down the field that results at radius r.

 

[SammyS]

This is A. But we don’t know r, only a and b .

Lots easier to read if you rotate the image and display it full size.

 

[rudransh verma]

Your first three equations are good, but next you need to add the isolated charge at the centre to get the total charge contained inside radius r.
Next, write down the field that results at radius r.

 

[haruspex]

Ok, and what value of A makes that a constant?

 

[rudransh verma]

Ok, and what value of A makes that a constant?

q should be zero in the eqn of E ?

 

[haruspex]

q should be zero in the eqn of E ?

No, there would still be an r in the expression. You need to find a value of A such that there is no r in the expression for the field.
The way you left matters in the attachment might be obscuring it. Don’t plug in the numeric value of the central charge, leave it as Q, say. But replace q with the expression for that which you got by integration, i.e. the first line of the attachment.

 

[rudransh verma]

No, there would still be an r in the expression. You need to find a value of A such that there is no r in the expression for the field.
The way you left matters in the attachment might be obscuring it. Don’t plug in the numeric value of the central charge, leave it as Q, say. But replace q with the expression for that which you got by integration, i.e. the first line of the attachment.

 

[haruspex]

I didn't check the numbers at the end, but the algebra is right.
In hindsight, what did you find difficult about the question? Did you not really understand what was being asked?

 

[rudransh verma]

what did you find difficult about the question? Did you not really understand what was being asked?

What is A? Is it area or surface charge density?
Other questions are in picture!

 

[haruspex]

What is A? Is it area or surface charge density?
Other questions are in picture!

$\rho dV=dq$ is just the definition of charge density. A volume element of size dV in a region where the charge density is $\rho$ has charge $\rho dV$.

Consider a spherical shell element radius r, thickness dr. It has volume $dV=4\pi r^2dr$, and the charge density there is given as A/r, where A is some unknown constant. (You can think of it as an area density, but it doesn't need to be anything of natural physical significance. We might have been told the density is any strange function of r.)

We are asked to find a value for A such that the field within the charged shell has constant magnitude. Obviously the field is spherically symmetric, so we can take it as radial.
This means we need a general formula for the field at any given point between radii a and b. It is not adequate to find an A that makes the field the same at a and b (though that would probably lead to the same answer).

There are two ways to proceed from here. We can find the total charge inside radius r (including the isolated charge), then write down the field that produces at radius r, or we can find the field at r due to charge in the shell from a to r and add the field due to the isolated charge. The result will be the same.
I chose one, the solution at your link chose the other.

Anything else?

 

[rudransh verma]

ρdV=dq is just the definition of charge density. A volume element of size dV in a region where the charge density is ρ has charge ρdV.

But dq/dV is not a fraction. It’s the change in q with a small change in V. Someone said d/dV is a operator. But we also know dq/dV is defined as a slope. There is some confusion!

Consider a spherical shell element radius r, thickness dr. It has volume dV=4πr2dr,

If the shell element has a thickness then how will it have constant radius r through its thickness. Is dr so small that we say it has constant r at all points in element.

 

[haruspex]

But dq/dV is not a fraction. It’s the change in q with a small change in V

It is the limit of a sequence of fractions. For a small change ΔV in V, Δq is the change in q. dq/dV is the limit of Δq/ΔV as ΔV tends to zero.

If the shell element has a thickness then how will it have constant radius r through its thickness. Is dr so small that we say it has constant r at all points in element.

Yes. If you write it all out exactly you get second order small terms, which can be ignored in the limit. That's how calculus works.

 

[rudransh verma]

It is the limit of a sequence of fractions. For a small change ΔV in V, Δq is the change in q. dq/dV is the limit of Δq/ΔV as ΔV tends to zero.

“Wikipedia has a nice explanatory article on the term rate here. The first paragraph states

“In mathematics, a rate is the ratio between two related quantities in different units.[1] If the denominator of the ratio is expressed as a single unit of one of these quantities, and if it is assumed that this quantity can be changed systematically (i.e., is an independent variable), then the numerator of the ratio expresses the corresponding rate of change in the other (dependent) variable.” “
This is a paragraph from a link.
I want to ask. When we say rate is dq/dV then it’s the limit of a fraction. As h/deltaV tends to zero we put h=0 and we get the value of f(x+h)-f(x). This is the rate dq/dV.
Right?

 

[haruspex]

“Wikipedia has a nice explanatory article on the term rate here. The first paragraph states

“In mathematics, a rate is the ratio between two related quantities in different units.[1] If the denominator of the ratio is expressed as a single unit of one of these quantities, and if it is assumed that this quantity can be changed systematically (i.e., is an independent variable), then the numerator of the ratio expresses the corresponding rate of change in the other (dependent) variable.” “
This is a paragraph from a link.
I want to ask. When we say rate is dq/dV then it’s the limit of a fraction. As h/deltaV tends to zero we put h=0 and we get the value of f(x+h)-f(x). This is the rate dq/dV.
Right?

Putting it in that notation, we have two functions of radius:
q = q(r), the total charge within radius r
V = V(r), the total volume within radius r
If we extend the radius by h (or 'Δr') then the contained quantities become q(r+Δr), V(r+Δr).
The rates of change with respect to r are the limits of (q(r+Δr)-q(r))/Δr as Δr tends to zero, etc.
These we write as dq/dr, etc.
To get the rate of change of the charge with respect to changes in volume we can instead write
$\frac{q(r+Δr)-q(r)}{V(r+Δr)-V(r)}=\frac{(q(r+Δr)-q(r))/Δr}{(V(r+Δr)-V(r))/Δr}$. In the limit, $\frac{dq}{dV}=\frac{dq/dr}{dV/dr}$.
So you can treat these like normal fractions, mostly.

 

[rudransh verma]

To get the rate of change of the charge with respect to changes in volume we can instead write
q(r+Δr)−q(r)V(r+Δr)−V(r)=(q(r+Δr)−q(r))/Δr(V(r+Δr)−V(r))/Δr. In the limit, dqdV=dq/drdq/dV.
So you can treat these like normal fractions, mostly.

Eg: The speed is a ratio of distance/ time. It gives us some quantity in m/km per unit sec/hour. This is rate. In the same way delta q/ delta V or delta q/ delta r or delta V/ delta r alone gives us rate. Why take limit and unnecessarily call it dq/dV or dq/dr etc.

 

[haruspex]

Eg: The speed is a ratio of distance/ time. It gives us some quantity in m/km per unit sec/hour. This is rate. In the same way delta q/ delta V or delta q/ delta r or delta V/ delta r alone gives us rate. Why take limit and unnecessarily call it dq/dV or dq/dr etc.

If you measure how far you have travelled, $\Delta x$, in some time $\Delta t$ then take the ratio $\frac{\Delta x}{\Delta t}$, it gives you the average speed over time $\Delta t$. To get the instantaneous speed at some instant t we need to take the limit as $\Delta t$ tends to zero.

 

[rudransh verma]

If you measure how far you have travelled, $\Delta x$, in some time $\Delta t$ then take the ratio $\frac{\Delta x}{\Delta t}$, it gives you the average speed over time $\Delta t$. To get the instantaneous speed at some instant t we need to take the limit as $\Delta t$ tends to zero.

So delta q/ delta V is average rate. To get instantaneous we need limit. But when we take smaller and smaller delta V we get smaller and smaller slopes ie more precise rate(exactly what we need). Then we take limit. We put h=0. Why doesn’t this makes the delta q zero because they are exactly the same points. How do we get instantaneous rate dq/dV. What is the mechanism of limit ?

 

[haruspex]

when we take smaller and smaller delta V we get smaller and smaller slopes

No, they can converge to a nonzero value.
Consider the point (1,1) on the curve $y=x^2$. The average gradient from there to $(1+s,(1+s)^2)$ is $\frac{(1+s)^2-1}{(1+s)-1}=2+s$. Taking the limit as s tends to zero gives a gradient of 2.

We put h=0

No, we don't set it equal to zero. That would give 0/0, which is indeterminate. We take the limit as it approaches zero.
To take this further, you need to take a course on limits.

 

[rudransh verma]

No, they can converge to a nonzero value.
Consider the point (1,1) on the curve $y=x^2$. The average gradient from there to $(1+s,(1+s)^2)$ is $\frac{(1+s)^2-1}{(1+s)-1}=2+s$. Taking the limit as s tends to zero gives a gradient of 2.

No, we don't set it equal to zero. That would give 0/0, which is indeterminate. We take the limit as it approaches zero.
To take this further, you need to take a course on limits.

I have read some limits. Now it’s coming to me. Yes here it converges to 2. But only when we have arranged it so that it doesn’t yield 0 in the denominator. Now we can put s =0. So here dy/dx= 2. That is defined as slope of the tangent at the point (1,1) where we need to find the rate. This rate only comes when we take limit. And here slope is 2. Right?

Also in #post 21 there should be dV/dr.

 

[haruspex]

I have read some limits. Now it’s coming to me. Yes here it converges to 2. But only when we have arranged it so that it doesn’t yield 0 in the denominator. Now we can put s =0. So here dy/dx= 2. That is defined as slope of the tangent at the point (1,1) where we need to find the rate. This rate only comes when we take limit. And here slope is 2. Right?

Yes.

 

[rudransh verma]

Yes.

Also in #post 21 there should be dV/dr.

 

[haruspex]

Also in #post 21 there should be dV/dr.

Ah yes - corrected.

 

[rudransh verma]

We are asked to find a value for A such that the field within the charged shell has constant magnitude. Obviously the field is spherically symmetric, so we can take it as radial.
This means we need a general formula for the field at any given point between radii a and b. It is not adequate to find an A that makes the field the same at a and b (though that would probably lead to the same answer).

Why is the question telling us that field inside to be uniform. Is there a field inside the shell. How do we calculate that?
We know only that the spherical non conducting shell produce E=1/(4pie0)q/r^2 outside the surface of shell as if the charge is at the center(shell theorem1) where q is spread out in the shell unlike a conductor where the charge resides at the external surface.
Also charges don’t induce because it’s a nonconductor with charge Q at the center.