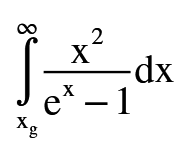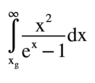SUMMARY
The integral of the function x²/(e^x - 1) from xg to infinity does not have a closed form. However, if xg is greater than 1, it can be approximated by the integral ∫(x²/e^x)dx from xg to infinity, which simplifies to (xg² + 2xg + 2)/e^(xg). This approximation becomes increasingly accurate as xg moves further from 1, with significant agreement observed for xg values of 5 or greater, matching numerical results from Wolfram Alpha.
PREREQUISITES
- Understanding of integral calculus, specifically improper integrals.
- Familiarity with exponential functions and their properties.
- Knowledge of integration techniques, including integration by parts.
- Experience with numerical integration methods and tools like Wolfram Alpha.
NEXT STEPS
- Explore the properties of improper integrals and convergence criteria.
- Learn about integration by parts and its applications in solving complex integrals.
- Investigate numerical integration techniques for approximating integrals without closed forms.
- Study the behavior of exponential functions in limit processes and their implications in calculus.
USEFUL FOR
Mathematicians, physics students, and anyone involved in advanced calculus or numerical analysis who seeks to understand complex integrals and their approximations.