How Do You Calculate Angular Frequency for a Sphere Oscillating in a Cylinder?

[Hernaner28]

Homework Statement

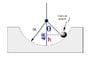
Esphere of radious R which oscilates inside a cylinder of radious 5R.
Calculate the angular frequency for small oscilations.

Homework Equations

The Attempt at a Solution

I hate Newton to solve SHM problems where weight is acting so I opted for energy but I cannot find out what's the gravitationall energy:

\displaystyle E=\frac{1}{2}I{{\omega }^{2}}+\frac{1}{2}M{{v}^{2}}+Mgh

\displaystyle E=\frac{7}{4}M{{{\dot{x}}}^{2}}+Mgh

Plz helP! Thanks!

 

[LawrenceC]

Assume a small angle from the vertical for the sphere release point. The height is the difference in elevations of its center of mass as it moves from the release point to the bottom of the cylinder.

 

[Hernaner28]

How is that written down as the gravitational energy? I'm really confused. The problem doesn't say anything about the release point so I don't know the height

Thank you

 

[Hernaner28]

Could you please type the equation for energy? I have a test in 2 hour and I'm in a hurry.. I need to understand this. just this time please!

 

[Hernaner28]

Alright, now I wrote:

\displaystyle E=\frac{1}{2}I\dot{\theta }+\frac{1}{2}M{{\left( \dot{\theta }R \right)}^{2}}-4R\cos \theta Mg

But the result I got is not option B ! I get that the angular frequency is 10g/3R

 

[Yukoel]

Alright, now I wrote:

\displaystyle E=\frac{1}{2}I\dot{\theta }+\frac{1}{2}M{{\left( \dot{\theta }R \right)}^{2}}-4R\cos \theta Mg

But the result I got is not option B ! I get that the angular frequency is 10g/3R

Hello Hernaner28,
The energy equation you wrote in the attempt section of your opening post is correct.But you are misinterpreting it I suspect by the looks of your method.This is angular SHM no doubt.But which angle is involved here? The elevation from central line or that in the body?
As LawrenceC says you need to know what actual height of your Center of Mass is.The body is translating and rotating at the same time , so for the sake of energy conservation for a SHM you need to assume it is rolling.Then frame the necessary condition for rolling and you are done.

regards
Yukoel

 

[ehild]

Alright, now I wrote:

\displaystyle E=\frac{1}{2}I\dot{\theta }+\frac{1}{2}M{{\left( \dot{\theta }R \right)}^{2}}-4R\cos \theta Mg

But the result I got is not option B ! I get that the angular frequency is 10g/3R

The small ball performs small oscillations around its equilibrium position, that is, the deepest point. So it is practical to define the angle variable from that point, as in the picture to ensure it small. Also you can define the zero of gravitational potential energy from he deepest position of the CM.

When writing up the kinetic energy attributed to the motion of CM its velocity is the radius of the circular motion (4R) times dθ/dt . You wrote Rdθ/dt.


ehild

 

[amiras]

There is no right answer here, assuming body to be hollow sphere with moment of inertia 2/3 mr^2 and gravitational potential energy 0 at the equilibrium position. According to the picture ehild provided.

Equation of motion:

1/2 Iω^2 + 1/2 m(4rω)^2 -(5-4cosθ)mgR = 1/2 ω^2 (I + 16mr^2) - (5-4cosθ)mgR = 0

Differentiating with respect of θ or t gives.

θ''(I + 16mr^2) -4mgR sinθ=0

or

θ'' = 4mgR sinθ/ (I + 16mr^2)

Assuming I = 2/3mr^2

θ'' = 4g/(2/3 r+16r) sinθ = 4/(50/3) g/r sinθ = 6g/(25r) sinθ

Assuming full ball, I = 2/5 mr^2

θ'' = 4g/(2/5 r+16r) sinθ = 4/(82/5) g/r sinθ = 10g/(41r) sinθ

 

[Yukoel]

There is no right answer here, assuming body to be hollow sphere with moment of inertia 2/3 mr^2 and gravitational potential energy 0 at the equilibrium position. According to the picture ehild provided.

Equation of motion:

1/2 Iω^2 + 1/2 m(4rω)^2 -(5-4cosθ)mgR = 1/2 ω^2 (I + 16mr^2) - (5-4cosθ)mgR = 0

Differentiating with respect of θ or t gives.

θ''(I + 16mr^2) -4mgR sinθ=0

or

θ'' = 4mgR sinθ/ (I + 16mr^2)

Assuming I = 2/3mr^2

θ'' = 4g/(2/3 r+16r) sinθ = 4/(50/3) g/r sinθ = 6g/(25r) sinθ

Assuming full ball, I = 2/5 mr^2

θ'' = 4g/(2/5 r+16r) sinθ = 4/(82/5) g/r sinθ = 10g/(41r) sinθ

Hello amiras,
Nice attempt.However you have to notice two things here.
(1) The ω w.r.t the curvature's center and that w.r.t the body are different. I mean the sphere's rotational energy uses a different ω in its expression than the ω used for the variation of θ i.e. the elevation with respect to the central line.These two angular velocities have a definite ratio.
(2)I might be getting your method wrong but the center of mass of the sphere remains constrained in a circle of radius 4 .So the expression for gravitational potential energy is different right?Or to be more precise the expression is simpler a little bit.It gets corrected however when you differentiate.
I think there is a correct answer among those options given.(assuming a solid sphere of course)
The restoring force method is much better here in this situation.The energy method also works anyway.

regards
Yukoel

 

[ehild]

I think there is a correct answer among those options given.(assuming a solid sphere of course)
The restoring force method is much better here in this situation.The energy method also works anyway.

regards
Yukoel

Yes, the correct answer is among the options.
And the easiest way for me is using the Lagrangian.

ehild

 

[amiras]

Hello amiras,
Nice attempt.However you have to notice two things here.
(1) The ω w.r.t the curvature's center and that w.r.t the body are different. I mean the sphere's rotational energy uses a different ω in its expression than the ω used for the variation of θ i.e. the elevation with respect to the central line.These two angular velocities have a definite ratio.
(2)I might be getting your method wrong but the center of mass of the sphere remains constrained in a circle of radius 4 .So the expression for gravitational potential energy is different right?Or to be more precise the expression is simpler a little bit.It gets corrected however when you differentiate.
I think there is a correct answer among those options given.(assuming a solid sphere of course)
The restoring force method is much better here in this situation.The energy method also works anyway.

regards
Yukoel

About this kinetic energy, let's say:

K = 1/2 m(v_cm)^2 + 1/2 I(ω_r)^2

Now v_cm = 4Rω = 4Rθ'

And ω_r = 5θ' ?

That does not give the right result, I'm confused.

 

[Yukoel]

About this kinetic energy, let's say:

K = 1/2 m(v_cm)^2 + 1/2 I(ω_r)^2

Now v_cm = 4Rω = 4Rθ'

And ω_r = 5θ' ?

That does not give the right result, I'm confused.

Hello amiras,
Once again notice that the center of mass of sphere moves in a circle of radius 4 R w.r.t. the center of cylindrical surface.Apply the condition of rolling on sphere's velocity and angular velocity and use the correct expression of tangential velocity .(w.r.t the center of cylindrical surface).
V_cm is defined correctly.
ω_R needs a revision

You should be getting a different constant as a multiplier instead of 5.Can you work out what it is?
regards
Yukoel

 

[amiras]

Hello amiras,
Once again notice that the center of mass of sphere moves in a circle of radius 4 R w.r.t. the center of cylindrical surface.Apply the condition of rolling on sphere's velocity and angular velocity and use the correct expression of tangential velocity .(w.r.t the center of cylindrical surface).
V_cm is defined correctly.
ω_R needs a revision

You should be getting a different constant as a multiplier instead of 5.Can you work out what it is?
regards
Yukoel

I can't possibly understand why this ratio ω_r/θ' is not 5.

I imagine a full cylinder of radius R lying lying on its side, and inside of it a sphere of radius r.
Lets say that we rotate the cylinder with an angle θ, and because of that the sphere rotates with angle β. Now they both did rotated the same distance Rθ=rβ
Differentiating both sides gives: Rθ' = rβ' or β'/θ' = R/r, in this case R=5r so it would give the ratio of 5.

 

[ehild]

I can't possibly understand why this ratio ω_r/θ' is not 5.

I imagine a full cylinder of radius R lying lying on its side, and inside of it a sphere of radius r.
Lets say that we rotate the cylinder with an angle θ, and because of that the sphere rotates with angle β. Now they both did rotated the same distance Rθ=rβ
Differentiating both sides gives: Rθ' = rβ' or β'/θ' = R/r, in this case R=5r so it would give the ratio of 5.

The sphere rolls inside the cylinder. The condition of rolling is: the length of arc traveled by the CM is the same as covered by the rim of the ball. The CM moves along a circle of radius 4R.

ehild

 

[amiras]

The sphere rolls inside the cylinder. The condition of rolling is: the length of arc traveled by the CM is the same as covered by the rim of the ball. The CM moves along a circle of radius 4R.

ehild

Thanks! I never knew this condition, but after some geometrical drawing I understand it now. Again, thanks for help, great community.

 

[ehild]

You are welcome. To tell the truth, I thought the same way as you, but I
cut out a small circle and rolled it inside a big one and I got enlightened

ehild

 

[Hernaner28]

The small ball performs small oscillations around its equilibrium position, that is, the deepest point. So it is practical to define the angle variable from that point, as in the picture to ensure it small. Also you can define the zero of gravitational potential energy from he deepest position of the CM.

When writing up the kinetic energy attributed to the motion of CM its velocity is the radius of the circular motion (4R) times dθ/dt . You wrote Rdθ/dt. ehild

I don't understand why I have to take 4R and not R. The sphere as a translation speed which is the one defined by the rolling without slipping condition and the radius of the esphere is R, not 4R.

Thanks.

And the correct option for you to know is B.

 

[ehild]

You took theta as the angle of rotation of the sphere, did you? In that case, multiplying with R is correct in the kinetic energy terms, but revise the potential energy.

ehild

 

[Hernaner28]

Theta is the angular displacement of the ball as if it was a pendulum. The angle you shown in your diagram. But why is the potential energy wrong? I took that the potential energy in the equilibrium position (vertical) is -4R. So the potential energy when the ball has displaced an angle of theta is -4Rcos(theta).

Thanks

 

[ehild]

If theta is the angle shown in my diagram then it also shows the position of the CM of the sphere. The CM of the sphere moves along a circle of radius 4R. Its speed is 4Rdθ/dt.

ehild

 

[Yukoel]

Theta is the angular displacement of the ball as if it was a pendulum. The angle you shown in your diagram. But why is the potential energy wrong? I took that the potential energy in the equilibrium position (vertical) is -4R. So the potential energy when the ball has displaced an angle of theta is -4Rcos(theta).

Thanks

Hello Hernaner28,
It depends on where you define the position of gravitational potential energy to be zero.I defined it zero at the C.O.M of the sphere at the bottom.You define it at the center of the cylindrical surface I assume.It does not finally affect your energy equation because the position adds the a constant to your P.E. at best.You get rid of it after differentiation.You are correct here ,not wrong.Have you tried the restoring force method to solve this too by the way.The algorithm there is pretty much the same as here, the only difference being the calculation of the acceleration of a rolling body on an approximated incline.

regards
Yukoel

 

[Yukoel]

I don't understand why I have to take 4R and not R. The sphere as a translation speed which is the one defined by the rolling without slipping condition and the radius of the esphere is R, not 4R.

Thanks.

And the correct option for you to know is B.

Hello Hernaner28,
There are two rotations (to be exact) in this diagram.Yes for applying the slipping condition you take only R w.r.t the sphere's angular velocity all by itself.Here you get one expression for C.O.M isn't it?Look again , draw a line joining the center of the sphere to the center of sphere.What is the distance here? The C.O.M as ehild says is executing circular motion around the center of cylindrical surface.The velocity of C.O.M of sphere gets another expression for itself depending upon the angular velocity w.r.t the central line of the cylinder. The expressions are then to be equated for the relation between these angular velocities.
Hoping this helps.
regards
Yukoel

 

[Hernaner28]

If theta is the angle shown in my diagram then it also shows the position of the CM of the sphere. The CM of the sphere moves along a circle of radius 4R. Its speed is 4Rdθ/dt.

ehild

Yeah, but the sphere is also rolling, and the condition is that:

\displaystyle {{v}_{CM}}=R\frac{d\theta }{dt}

That is not wrong. But if you tell me that it's 4Rdθ/dt then it's the same as saying:

\displaystyle {{v}_{CM}}=R\frac{d\theta }{dt}=4R\frac{d\theta }{dt}

which is definitely not the same. What is wrong about taking into account the non-slip condition? Then it would be the same if it didn't roll !