- 1,753
- 143
In the circuit shown, find the current in each resistor and the values of the potential at points A, B, and C.
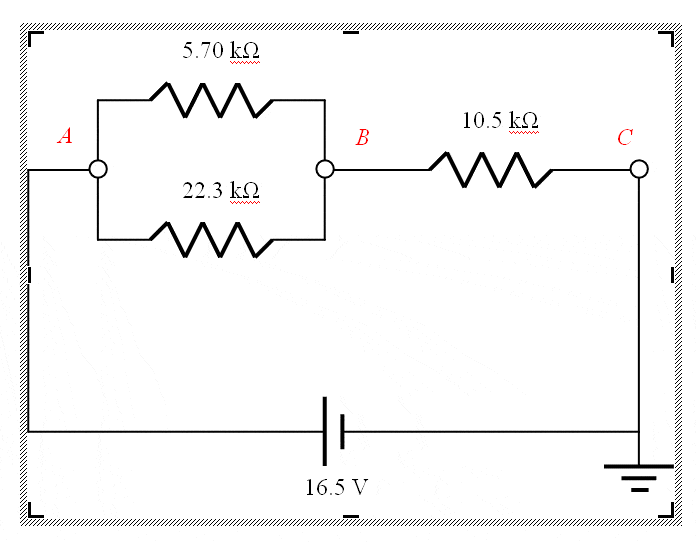
First I computed the combined resistance of the parallel resistors and got 4.54 kOhms. Then I added this to 10.5 to get 15.04 kOhms total resistance.
So from Ohm's law, the total current is I=V/R = 16.5 / 15040 = 1.0971 x 10-3 A.
I get potentials at A, B, and C of 16.5, 11.5, and 0 volts.
I think this is correct so far.
To find the current through each resistor:
For the 10.5 kOhm resistor, since it is in series, it makes sense to me that the current through this resistor must be equal to the total current: 1.0971 x 10-3 A. And that the current running through the parallel pair must also be 1.0971 x 10-3 A. But the voltage across this resistor is 16.5-11.5, or 5v. Using Ohm's law, I=V/R, I get 5/10500 = 0.000476 A
Which way is correct?
Thanks
First I computed the combined resistance of the parallel resistors and got 4.54 kOhms. Then I added this to 10.5 to get 15.04 kOhms total resistance.
So from Ohm's law, the total current is I=V/R = 16.5 / 15040 = 1.0971 x 10-3 A.
I get potentials at A, B, and C of 16.5, 11.5, and 0 volts.
I think this is correct so far.
To find the current through each resistor:
For the 10.5 kOhm resistor, since it is in series, it makes sense to me that the current through this resistor must be equal to the total current: 1.0971 x 10-3 A. And that the current running through the parallel pair must also be 1.0971 x 10-3 A. But the voltage across this resistor is 16.5-11.5, or 5v. Using Ohm's law, I=V/R, I get 5/10500 = 0.000476 A
Which way is correct?
Thanks