issacnewton
- 1,035
- 37
A 3 kg cafe sign is to be hung from 1 kg horizontal beam such that it is in equilibrium. The beam is 4 m long. A wire is attached to the beam at its right end to prevent the sign and the beam from rotating. The beam is pressed against the wall on its left end and is prevented from sliding by a bracket that is fixed to the wall.
a) What is the tension force in the wire ?
b) What is the normal force of the wall pushing against the left end of the beam ?
c) What is the upward force supporting the left end of the beam ?
d) How far from the wall should sign be hung so that it is in equilibrium ?
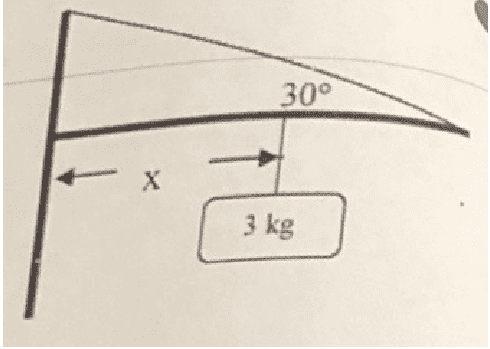
Now following is my attempt at solution. Let ##T## be the tension in the wire and ##\theta = 30 ^{\circ}## be the angle made by the wire with the horizontal. Let ##F## be the upward force supporting the left end of the beam and ##N## be the normal force of the wall pushing against the left end of the beam. Let ##L=4m## be the length of the beam and ##M = 1 kg## be the mass of the beam and ##m=3 kg## be the mass of the cafe sign. Then the condition that the net force on the beam is zero leads to the following equations
$$ N = T\cos(\theta) \cdots\cdots (1)$$
$$ F + T \sin(\theta) = Mg + mg \cdots\cdots (2)$$
Now, the net torque about the right end of the beam is zero. So this leads to the equation
$$ Mg(L/2) +mg(L-x) - FL = 0 \cdots\cdots (3) $$
Also, the net torque about the leftend of the beam is zero. So this leads to the equation
$$ T \sin(\theta) L -Mg(L/2) - mg x = 0 \cdots\cdots (4) $$
Now, it seems that, these four equations are not sufficient to entirely solve this problem with four unknowns ##F,N,T,x##. I just get three equations and 4 unknowns after doing some algebra. So any hints here ?
a) What is the tension force in the wire ?
b) What is the normal force of the wall pushing against the left end of the beam ?
c) What is the upward force supporting the left end of the beam ?
d) How far from the wall should sign be hung so that it is in equilibrium ?
Now following is my attempt at solution. Let ##T## be the tension in the wire and ##\theta = 30 ^{\circ}## be the angle made by the wire with the horizontal. Let ##F## be the upward force supporting the left end of the beam and ##N## be the normal force of the wall pushing against the left end of the beam. Let ##L=4m## be the length of the beam and ##M = 1 kg## be the mass of the beam and ##m=3 kg## be the mass of the cafe sign. Then the condition that the net force on the beam is zero leads to the following equations
$$ N = T\cos(\theta) \cdots\cdots (1)$$
$$ F + T \sin(\theta) = Mg + mg \cdots\cdots (2)$$
Now, the net torque about the right end of the beam is zero. So this leads to the equation
$$ Mg(L/2) +mg(L-x) - FL = 0 \cdots\cdots (3) $$
Also, the net torque about the leftend of the beam is zero. So this leads to the equation
$$ T \sin(\theta) L -Mg(L/2) - mg x = 0 \cdots\cdots (4) $$
Now, it seems that, these four equations are not sufficient to entirely solve this problem with four unknowns ##F,N,T,x##. I just get three equations and 4 unknowns after doing some algebra. So any hints here ?