StephenDoty
- 261
- 0
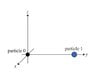
A. Consider two positively charged particles, one of charge q_0 (particle 0) fixed at the origin, and another of charge q_1 (particle 1) fixed on the y-axis at (0,d_1, 0). What is the net force F_vec on particle 0 due to particle 1?
Express your answer (a vector) using any or all of k, q_0, q_1, d_1, \hat{x}unit, \hat{y}unit, and \hat{z}unit. (See Picture CPartA)
F=kq0q1/d1^2 C and the vector is in the direction of -y so the F_vector = kq0q1/d1^2 C (-\hat{j}. But how do you put this into mastering physics? Do you use just the\hat{j} or do you put -\hat{j} at the end of F=kq0q1/d1^2?
B. Now add a third, negatively charged, particle, whose charge is -q_2 (particle 2). Particle 2 fixed on the y-axis at position (0,d_2,0). What is the new net force on particle 0, from particle 1 and particle 2?
Express your answer (a vector) using any or all of k, q_0, q_1, d_1, \hat{x}unit, \hat{y}unit, and \hat{z}unit. (See Picture CPartB)
The F on 0 due to 1 goes to the -y direction and the F on 0 due to 2 goes to the +y direction. Thus the F net = F on 0 due to 2 - F on 0 due to 1, since the negative charge is closer than the positive charge.
So F= (kq0q2/d2^2)-(kq0q1/d1^2) in the direction of \hat{j}. How do I input this answer into mastering physics?
C. Particle 0 experiences a repulsion from particle 1 and an attraction toward particle 2. For certain values of d_1 and d_2, the repulsion and attraction should balance each other, resulting in no net force. For what ratio d_1/d_2 is there no net force on particle 0?
Express your answer in terms of any or all of the following variables: k, q_0, q_1, q_2.
For the charges to have no net force on particle 0 the two forces must equal each other.
{(kq0q2)/d2^2} = {(kq0q1)/d1^2}
(d1^2/d2^2) = (kq0q1)/(kq0q2)
(d1^2/d2^2) = q1/q2
d1/d2= sqrt(q1/q2)
Do I just use the square root symbol in mastering physics and put q1/q2 in the parenthesis?
D. Now add a fourth charged particle, particle 3, with positive charge q_3, fixed in the yz-plane at (0,d_2,d_2). What is the net force F_vec on particle 0 due solely to this charge?
Express your answer (a vector) using k, q_0, q_3, d_2, x_unit, y_unit, and z_unit. Include only the force caused by particle 3. (See Picture CPartD)
The force on particle 0 due to q3 would be in the negative y and negative z and positive x direction. But I am unsure how to use F=kq0q3/r^2? Would r^2 be the distance, r^2= (d2^2)+(d2^2)? So would F = kq0q3/(d2^2+d2^2)? And how would I find the direction of the vector? Would it be the \hat{z} ? So I would put kq0q3/(2d2^2) \hat{z} into mastering physics?
Thank you for all of your help. I know I made a large message, but most of my questions are on how to input the answers into mastering physics. So any help would be appreciated. Thank you.
All of the pictures are attached.
Stephen
Express your answer (a vector) using any or all of k, q_0, q_1, d_1, \hat{x}unit, \hat{y}unit, and \hat{z}unit. (See Picture CPartA)
F=kq0q1/d1^2 C and the vector is in the direction of -y so the F_vector = kq0q1/d1^2 C (-\hat{j}. But how do you put this into mastering physics? Do you use just the\hat{j} or do you put -\hat{j} at the end of F=kq0q1/d1^2?
B. Now add a third, negatively charged, particle, whose charge is -q_2 (particle 2). Particle 2 fixed on the y-axis at position (0,d_2,0). What is the new net force on particle 0, from particle 1 and particle 2?
Express your answer (a vector) using any or all of k, q_0, q_1, d_1, \hat{x}unit, \hat{y}unit, and \hat{z}unit. (See Picture CPartB)
The F on 0 due to 1 goes to the -y direction and the F on 0 due to 2 goes to the +y direction. Thus the F net = F on 0 due to 2 - F on 0 due to 1, since the negative charge is closer than the positive charge.
So F= (kq0q2/d2^2)-(kq0q1/d1^2) in the direction of \hat{j}. How do I input this answer into mastering physics?
C. Particle 0 experiences a repulsion from particle 1 and an attraction toward particle 2. For certain values of d_1 and d_2, the repulsion and attraction should balance each other, resulting in no net force. For what ratio d_1/d_2 is there no net force on particle 0?
Express your answer in terms of any or all of the following variables: k, q_0, q_1, q_2.
For the charges to have no net force on particle 0 the two forces must equal each other.
{(kq0q2)/d2^2} = {(kq0q1)/d1^2}
(d1^2/d2^2) = (kq0q1)/(kq0q2)
(d1^2/d2^2) = q1/q2
d1/d2= sqrt(q1/q2)
Do I just use the square root symbol in mastering physics and put q1/q2 in the parenthesis?
D. Now add a fourth charged particle, particle 3, with positive charge q_3, fixed in the yz-plane at (0,d_2,d_2). What is the net force F_vec on particle 0 due solely to this charge?
Express your answer (a vector) using k, q_0, q_3, d_2, x_unit, y_unit, and z_unit. Include only the force caused by particle 3. (See Picture CPartD)
The force on particle 0 due to q3 would be in the negative y and negative z and positive x direction. But I am unsure how to use F=kq0q3/r^2? Would r^2 be the distance, r^2= (d2^2)+(d2^2)? So would F = kq0q3/(d2^2+d2^2)? And how would I find the direction of the vector? Would it be the \hat{z} ? So I would put kq0q3/(2d2^2) \hat{z} into mastering physics?
Thank you for all of your help. I know I made a large message, but most of my questions are on how to input the answers into mastering physics. So any help would be appreciated. Thank you.
All of the pictures are attached.
Stephen