How Do You Calculate Net Torque with Multiple Force-Couple Systems on a Beam?

[AngelofMusic]

This is a question about finding the resultant of the force system.

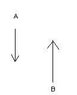
Basically, there is a rigid body with 3 pairs of forces with the same magnitude that are parallel to each other and in opposite directions. (I've attached an example of one of those pairs.) All three pairs are attached at different places on a long beam.

I converted one of the forces in each pair into a force-couple system. That means that each pair now has the forces cancelling each other out, and an additional moment (torque) vector.

(i.e. I moved the vector starting at A to point B, and found the torque of A once it has been moved to point B. Then the two forces cancel out.)

I was just wondering - do I also need to calculate the torque at point B when adding all the torques together? Since the torque is supposed to be a free vector, does that mean that all 3 of the resulting torques (with the pairs of forces in different places) can just be added together?

Also, since the forces are along the x and y axis, and the torques are perpendicular to that plane, would that make the resultant moment (torque) solely in the z-axis, then?

The textbook is incredibly confusing on this topic, and I'd appreciate any clarification!

 

[M98Ranger]

To find the resultant of a force system, you need to consider both the forces and the torques acting on the rigid body. In this case, you have correctly converted one of the forces in each pair into a force-couple system, meaning that you now have two forces acting on the body and an additional torque vector.

When adding all the torques together, you need to consider the sign of each torque. If the torques are in the same direction (clockwise or counterclockwise), you can simply add them together. However, if they are in opposite directions, you need to subtract them from each other. This will give you the net torque acting on the body.

Since the forces are along the x and y axis, and the torques are perpendicular to that plane, the resultant moment (torque) will indeed be solely in the z-axis. This is because the x and y components of the torques will cancel each other out, leaving only the z component as the net torque.

It is important to note that the torque is a free vector, meaning it can act at any point on the rigid body. Therefore, when calculating the resultant torque, you need to consider the torque at each point where the forces are acting. This will give you the total net torque acting on the body.

In conclusion, to find the resultant of a force system, you need to consider both the forces and the torques acting on the rigid body. The torques can be added or subtracted depending on their direction, and the resultant moment will be solely in the z-axis. It is important to consider the torque at each point where the forces are acting in order to calculate the total net torque.