How Do You Calculate Power Dissipation in a Double Loop Circuit?

[j_baby]

Homework Statement

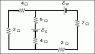
A double loop circuit is shown in the figure below.

The Emf εx = 7.00 V and the Emf εw = 17.00 V. Both are shown on the diagram. Calculate the power dissipated in the 7 Ω resistor located on the extreme right in the circuit.

The Attempt at a Solution

I always get confused with the direction this goes. I start out with the joint rule.
I1= I2 + I3 + I4 + I5 + I6

say I1 = the amps going through the seven ohm resister
I2 = " " that going through bottom 2 ohm
I3 = " " middle 4 ohm
I4 = " " middle 5 ohm
I5 = " " upper 4 ohm
I6 = " " left 2 ohm

Then I do one loop, say the rightmost
-7*I1 - 2*I2 - 4*I3 + 7V - 5*I4 - 17V = 0

then the right most loop
5*I4 -7V + 4*I3 - 2*I6 - 4*I5 = 0

is this the right way or completely wrong? any help would GREATLY be appreciated.. soon hah

 

[kamerling]

There are only 3 unknown currents in this circuit. The current through Ex and de 4 ohm and 5 ohm resistor above and below it is obviously the same. The same goes for the 4 and 2 ohms resistors on the left, and Ew and the 2 and 7 ohms resistors on the right

Kirchhoffs current law will give you one relationship between those currents. and using the voltage law on 2 loops will give you two more.