How Do You Calculate Spring Properties for Effective Landing Gear Design?

[Euan12345]

Summary:: I am making a landing gear mechanism, and am struggling to mathematically model it, the aim is to find the required properties for the spring for it to work.

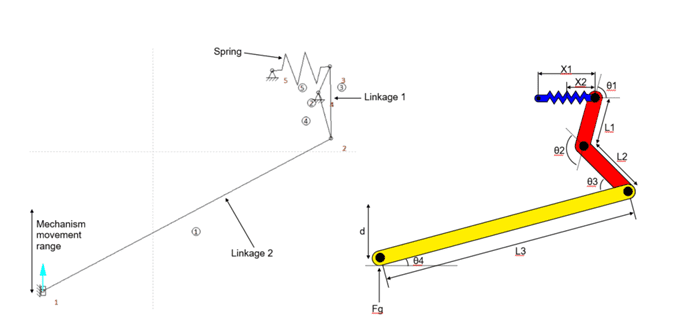
Hi can you help me with a problem, I am making a landing gear mechanism and am struggling to model it mathematically. The aim is to find the required properties for the spring, for it to work. The approach is based on the conservation of energy, and the frictional losses are assumed to be zero.

k - spring constant
X1 – initial spring length
X2 – Final spring length
W – work done
d – travel distance
L1, L2, L3 – constant length
Θ2 – constant
Θ1, θ3, θ4 – variable
Fg – force due to gravity

1 Finding work done by spring
Integrating Hooke’s law to express it in work done

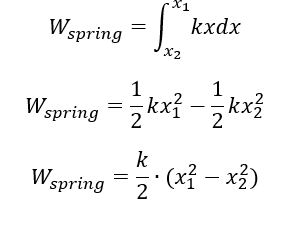
2 Finding forces acting on the mechanism

2.1 Calculating balanced moments
Since linkage 1 is balanced, the moments are equal to each other

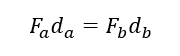
Adjusting for forces that aren’t acting tangential to the members of linkage 1.

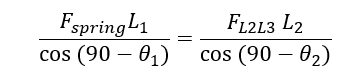
FL2L3 is the force acting linearly to the length of linkage 2

2.2 Adjusting for angled force
Finding relation between FL2L3 and Fg

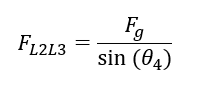
Inserting the relation into the equation, we have

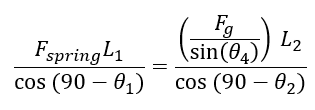
Rearranging

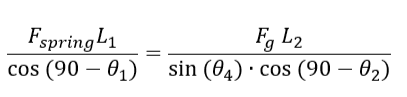
I don't know what to do from this point on, can you help with
1. Generally solving it?
2. How do you express all angles in terms of θ4?

Any help would be appreciated, thank you

 

[berkeman]

Should I move this thread to the schoolwork forums for you? Hopefully you are not trying to use the Internet to help you with your first landing gear design for a real aircraft, right?

 

[Lnewqban]

Where is the tire located at?
What does guide #1 to move vertically up and down?

 

[Euan12345]

Where is the tire located at?
What does guide #1 to move vertically up and down?

there are no tires, when I call it landing gear, I mean its suspension system used to absorb the impact of a falling object. there are multiple of them connected together with a ski like thing, that's why it has to act linearly

 

[Euan12345]

Should I move this thread to the schoolwork forums for you? Hopefully you are not trying to use the Internet to help you with your first landing gear design for a real aircraft, right?

please could you move it to the schoolwork form, I don't know how to do it

 

[Lnewqban]

there are no tires, when I call it landing gear, I mean its suspension system used to absorb the impact of a falling object. there are multiple of them connected together with a ski like thing, that's why it has to act linearly

Again, what does guide point #1 to move vertically up and down?
Shouldn't x2 be represented on the other end of the spring?
Why is force due to gravity decreasing?
Where da and db are located at?

It is very important to determine the spatial geometry of point #1 (and its range of free movement) respect to point #2.

 

[berkeman]

please could you move it to the schoolwork form, I don't know how to do it

Happy to.

 

[Baluncore]

The approach is based on the conservation of energy, and the frictional losses are assumed to be zero.

It would not land, I expect it would bounce back into the air again.
If it was to land, where does the bouncing energy go ?

 

[Euan12345]

Again, what does guide point #1 to move vertically up and down?
Shouldn't x2 be represented on the other end of the spring?
Why is force due to gravity decreasing?
Where da and db are located at?

It is very important to determine the spatial geometry of point #1 (and its range of free movement) respect to point #2.

1. it can only move along the y-axis (up and down)
2. your right, that's what I meant
3. that is another mistake, fixed it
4. da and db are meaningless lengths there just showing that the moment is balanced, I thought it was a bit of a leap so added that step

 

[Euan12345]

It would not land, I expect it would bounce back into the air again.
If it was to land, where does the bouncing energy go ?

I also intend to use a dampener in conjunction with the spring, I'm just disregarding that at this point as I am making a small scale (3D printable) basic concept prototype to test it.

 

[jack action]

• First, you got $F_b$ in terms of $\theta_2$, how is that even possible?
• Second, the relationship between $F_{L_2 L_3}$ - whatever it represents - and $F_g$ is most likely wrong.
• Third, I'm not sure why you need to analyze spring work at this point.

What you need to do is free body diagrams (FBD): one for linkage 1 and another one for linkage 2. You will have to assume that you have horizontal reactions on both:

• One on the slider connected to linkage 2;
• Another one on the center pin of linkage 1. There will also be a vertical force component on that pin.

To help you, instead of using $\theta_3$ as the angle between both linkages, define it as the angle between $L_2$ and the horizontal.

Although irrelevant for your free body diagram, note that the spring may be preloaded at a certain value of $\theta_1$. As long as $F_g$ does not counterbalance that preload force $F_p$, the mechanism will not move. (i.e. the pre-compressed spring is like a solid link). So once you find the force $F_s$ from linkage 1 acting on the spring - with your FBDs -, you can get the spring displacement between the final angle $\theta_{1f}$ and the initial angle $\theta_{1i}$ with (assuming the spring stays horizontal):
$$K L_1 (\cos \theta_{1i} - \cos \theta_{1f} ) = F_s - \min(F_s; F_{p\ @\theta_{1i}})$$
Where $K$ is the spring constant.

2. How do you express all angles in terms of θ4?

Once you have solved the FBDs, define $L_x$ as the horizontal distance between the slider and the center pin of linkage 1. Everything should come easy after that with simple geometry.