How Do You Calculate the Height of a Wedge in a Physics Problem?

[parwana]

A small block of mass m1 = 0.300 kg is released from rest at the top of a curved wedge of mass m2 = 2.00 kg, which sits on a frictionless horizontal surface as in Figure P6.59a. When the block leaves the wedge, its velocity is measured to be 4.00 m/s to the right, as in Figure P6.59b.

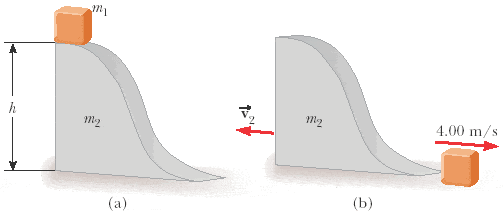
(a) What is the velocity of the wedge after the block reaches the horizontal surface?
I found the velocity to be -.6 m/s. I did 0=m2v2 + M(block)V(block)


(b) What is the height h of the wedge?
I don't know how to get the height of the wedge, please help

I know the energy equation will be

mgh= .5mv^2

Please help

 

[parwana]

please can anyone help?

 

[AVD]

If you find the velocity of the block and the wedge, you should be able to apply concervation of energy to determine the height of the wedge. This means one point you have to apply the formula to is when M1 is at rest at the top of the wedge. use mgh = (whatever you decide) to determine the height of M1 relative to the ground. This is the same as the height of the wedge.

 

[parwana]

I still don't understand. Can you show me how to set up the equation

Would it be

mgh= .5mv^2 Now which mass and which velocity should I use to find h here

 

[radou]

I still don't understand. Can you show me how to set up the equation

Would it be

mgh= .5mv^2 Now which mass and which velocity should I use to find h here

As AVD said, you have to use conservation of energy on the system consisting of the block and the wedge. So, write down the sum of kinetic and potential energy for these two momens and set them to equal one another; a) the block rests on the wedge, b) the block is on the horizontal surface.

 

[parwana]

^ I am really sorry, I tried setting it up but I am getting it wrong.

 

[rkslperez04]

would it be?

KE + PE = KE + PE

and go from there?

 

[parwana]

I tried that

.5(.3)(4^2) + .3(9.8)h= .5(32)(.6^2) + 2(9.8)h

is that right

It didnt work for some reason, I got .112 is height, or am I doing something wrong

 

[rkslperez04]

am I showing in notes from that this may be an inelastic collision (m1v1i + m2v2i = (m1 + m2)Vf)... sorry I am not help to you :(

 

[radou]

would it be?

KE + PE = KE + PE

and go from there?

PE(block) = KE(block) + KE(wedge), where PE(block) is for the moment the block is resting on the wedge, and KE(block) and KE(wedge) are for the moment when the block is on the horizontal surface, and the wedge has the velocity you calculated in part 1.

 

[parwana]

^ Its ok, I hope someone else helps

 

[parwana]

Thanks so much radou, but why don't we use the PE of the wedge?

 

[radou]

Thanks so much radou, but why don't we use the PE of the wedge?

The wedge has no potential energy, since it is on the horizontal surface all the time.

 

[parwana]

^ oh ok thanks a lot